C++编辑距离问题

编辑距离，也被称为 Levenshtein 距离，指两个字符串之间互相转换的最小修改次数，通常用于在信息检索和自然语言处理中度量两个序列的相似度。

如图 14-27 所示，将 kitten 转换为 sitting 需要编辑 3 步，包括 2 次替换操作与 1 次添加操作；将 hello 转换为 algo 需要 3 步，包括 2 次替换操作和 1 次删除操作。

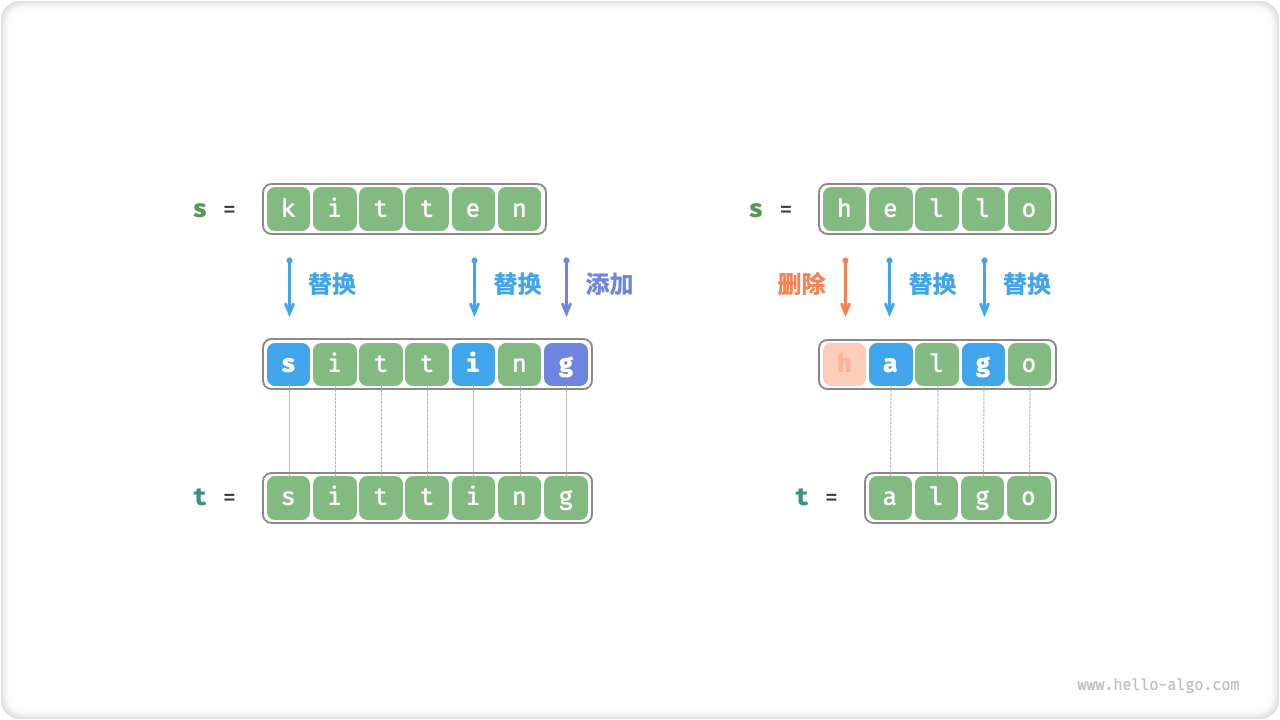
图 14-27   编辑距离的示例数据

编辑距离问题可以很自然地用决策树模型来解释。字符串对应树节点，一轮决策（一次编辑操作）对应树的一条边。

如图 14-28 所示，在不限制操作的情况下，每个节点都可以派生出许多条边，每条边对应一种操作，这意味着从 hello 转换到 algo 有许多种可能的路径。

从决策树的角度看，本题的目标是求解节点 hello 和节点 algo 之间的最短路径。

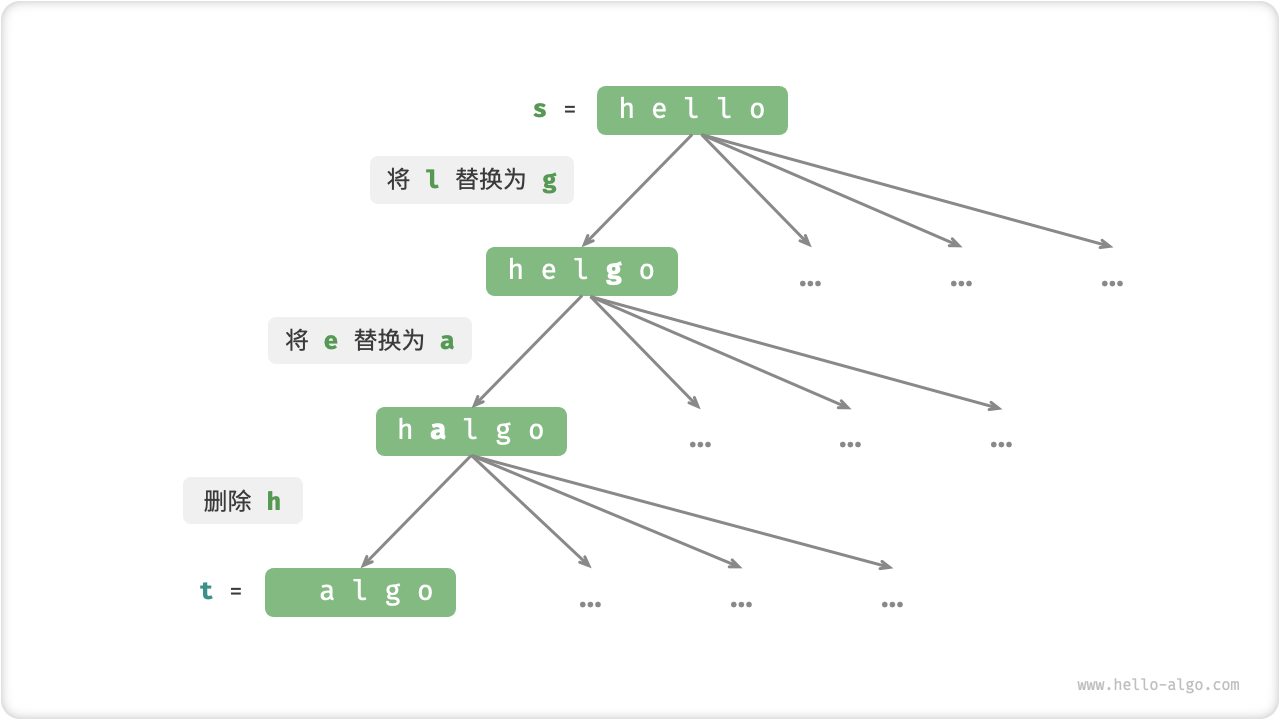
图 14-28   基于决策树模型表示编辑距离问题

1.   动态规划思路

第一步：思考每轮的决策，定义状态，从而得到 $dp$ 表

每一轮的决策是对字符串 $s$ 进行一次编辑操作。

我们希望在编辑操作的过程中，问题的规模逐渐缩小，这样才能构建子问题。设字符串 $s$ 和 $t$ 的长度分别为 $n$ 和 $m$ ，我们先考虑两字符串尾部的字符 $s[n-1]$ 和 $t[m-1]$ 。

• 若 $s[n-1]$ 和 $t[m-1]$ 相同，我们可以跳过它们，直接考虑 $s[n-2]$ 和 $t[m-2]$ 。
• 若 $s[n-1]$ 和 $t[m-1]$ 不同，我们需要对 $s$ 进行一次编辑（插入、删除、替换），使得两字符串尾部的字符相同，从而可以跳过它们，考虑规模更小的问题。

也就是说，我们在字符串 $s$ 中进行的每一轮决策（编辑操作），都会使得 $s$ 和 $t$ 中剩余的待匹配字符发生变化。因此，状态为当前在 $s$ 和 $t$ 中考虑的第 $i$ 和 $j$ 个字符，记为 $[i,j]$ 。

状态 $[i,j]$ 对应的子问题：将 $s$ 的前 $i$ 个字符更改为 $t$ 的前 $j$ 个字符所需的最少编辑步数。

至此，得到一个尺寸为 $(i+1)\times (j+1)$ 的二维 $dp$ 表。

第二步：找出最优子结构，进而推导出状态转移方程

考虑子问题 $dp[i,j]$ ，其对应的两个字符串的尾部字符为 $s[i-1]$ 和 $t[j-1]$ ，可根据不同编辑操作分为图 14-29 所示的三种情况。

1. 在 $s[i-1]$ 之后添加 $t[j-1]$ ，则剩余子问题 $dp[i,j-1]$ 。
2. 删除 $s[i-1]$ ，则剩余子问题 $dp[i-1,j]$ 。
3. 将 $s[i-1]$ 替换为 $t[j-1]$ ，则剩余子问题 $dp[i-1,j-1]$ 。

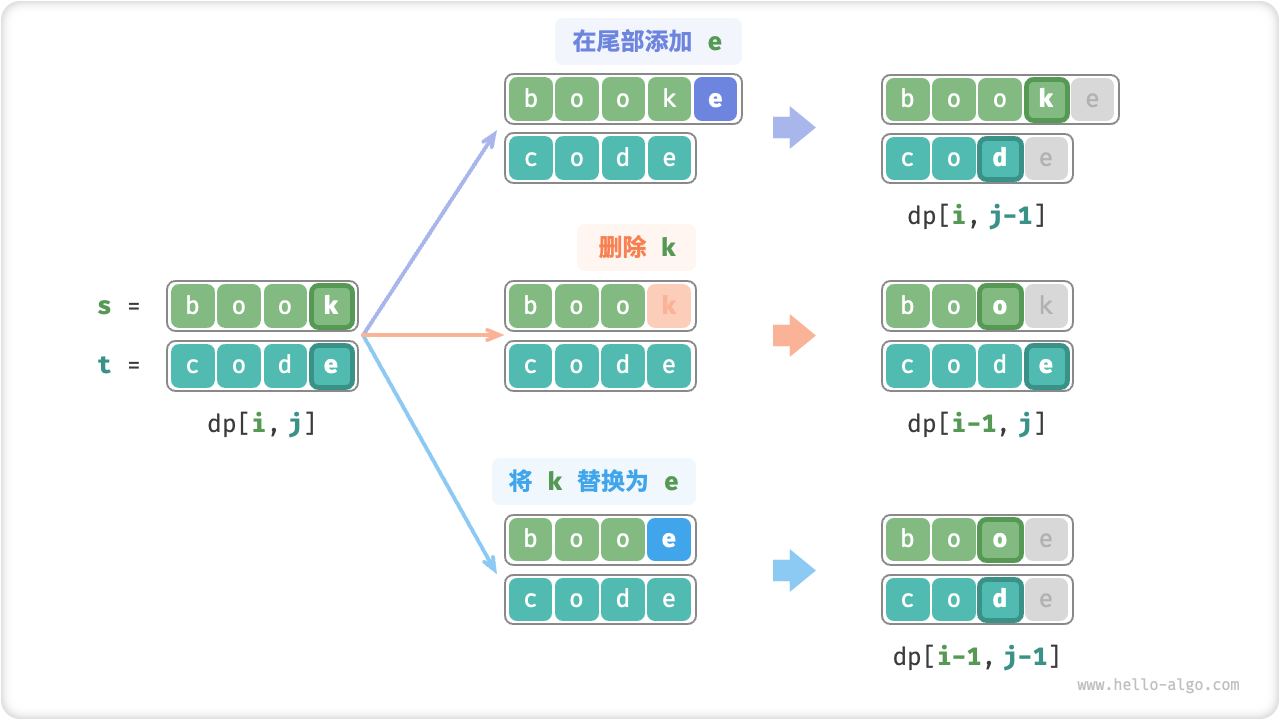
图 14-29   编辑距离的状态转移

根据以上分析，可得最优子结构：$dp[i,j]$ 的最少编辑步数等于 $dp[i,j-1]$、$dp[i-1,j]$、$dp[i-1,j-1]$ 三者中的最少编辑步数，再加上本次的编辑步数 $1$ 。对应的状态转移方程为：

请注意，当 $s[i-1]$ 和 $t[j-1]$ 相同时，无须编辑当前字符，这种情况下的状态转移方程为：

第三步：确定边界条件和状态转移顺序

当两字符串都为空时，编辑步数为 $0$ ，即 $dp[0,0]=0$ 。当 $s$ 为空但 $t$ 不为空时，最少编辑步数等于 $t$ 的长度，即首行 $dp[0,j]=j$ 。当 $s$ 不为空但 $t$ 为空时，等于 $s$ 的长度，即首列 $dp[i,0]=i$ 。

观察状态转移方程，解 $dp[i,j]$ 依赖左方、上方、左上方的解，因此通过两层循环正序遍历整个 $dp$ 表即可。

2.   代码实现

edit_distance.cpp

/* 编辑距离：动态规划 */
int editDistanceDP(string s, string t) {
    int n = s.length(), m = t.length();
    vector<vector<int>> dp(n + 1, vector<int>(m + 1, 0));
    // 状态转移：首行首列
    for (int i = 1; i <= n; i++) {
        dp[i][0] = i;
    }
    for (int j = 1; j <= m; j++) {
        dp[0][j] = j;
    }
    // 状态转移：其余行列
    for (int i = 1; i <= n; i++) {
        for (int j = 1; j <= m; j++) {
            if (s[i - 1] == t[j - 1]) {
                // 若两字符相等，则直接跳过此两字符
                dp[i][j] = dp[i - 1][j - 1];
            } else {
                // 最少编辑步数 = 插入、删除、替换这三种操作的最少编辑步数 + 1
                dp[i][j] = min(min(dp[i][j - 1], dp[i - 1][j]), dp[i - 1][j - 1]) + 1;
            }
        }
    }
    return dp[n][m];
}

如图 14-30 所示，编辑距离问题的状态转移过程与背包问题非常类似，都可以看作是填写一个二维网格的过程。

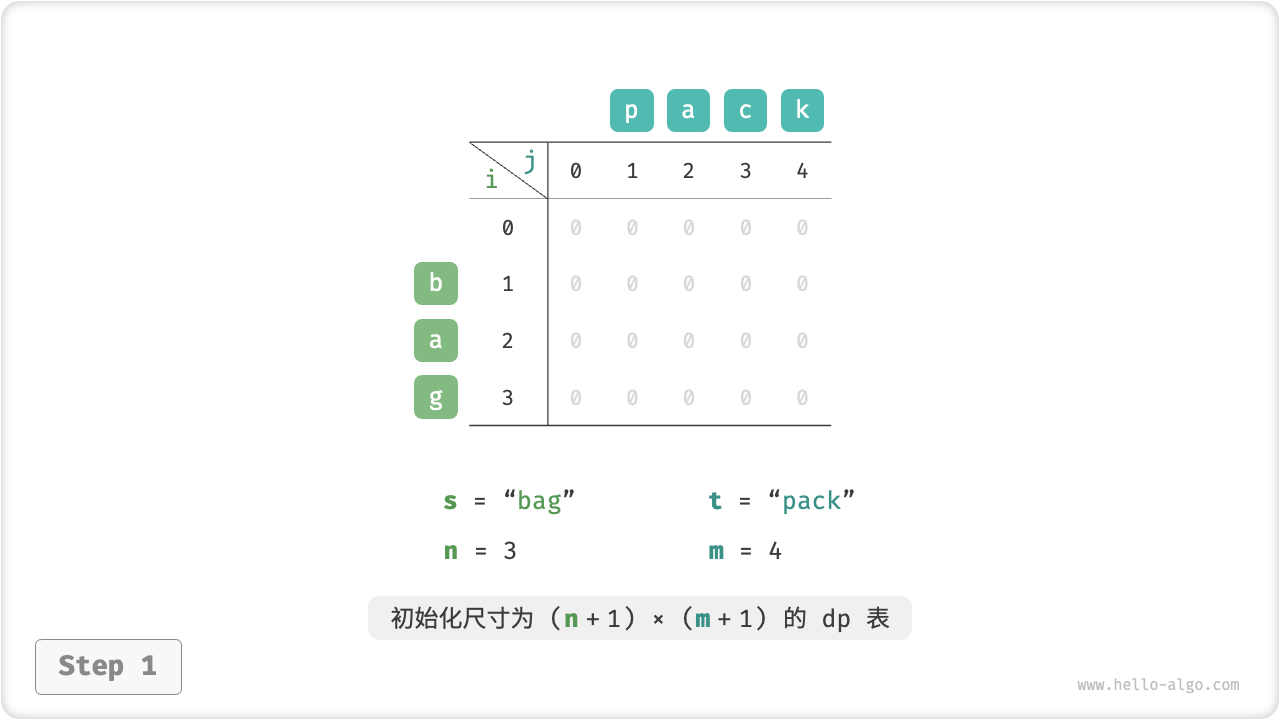
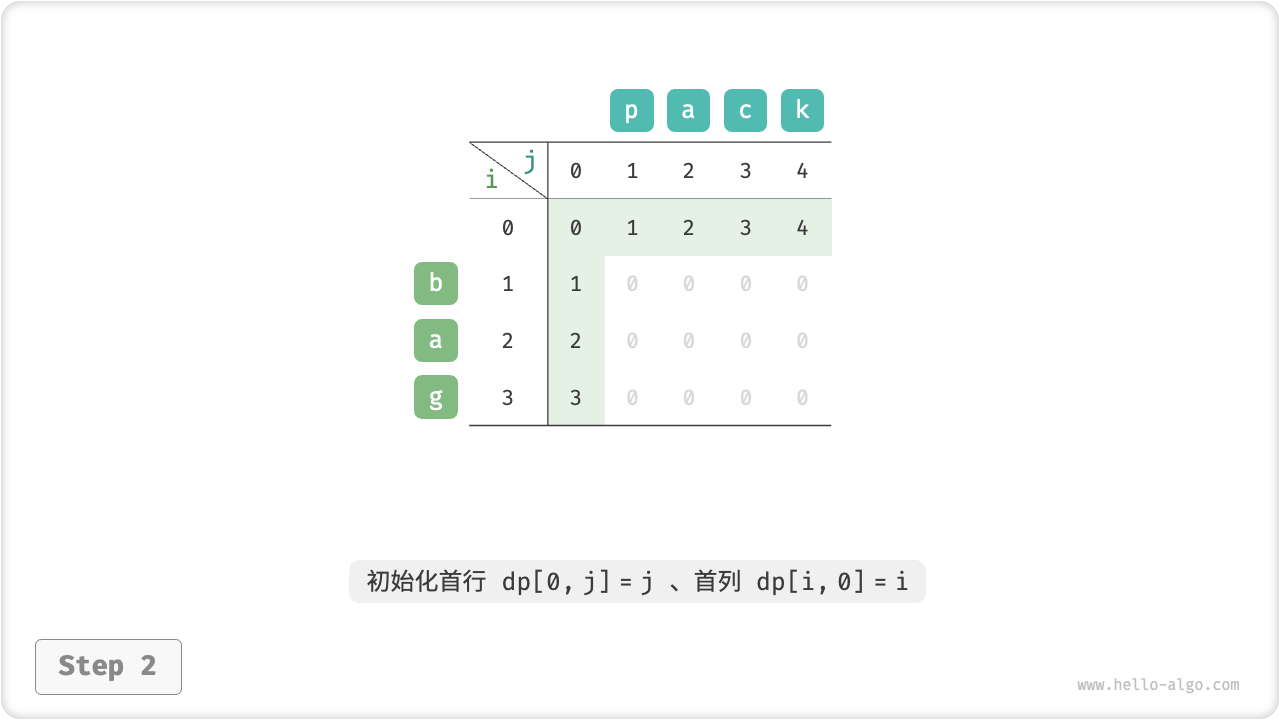
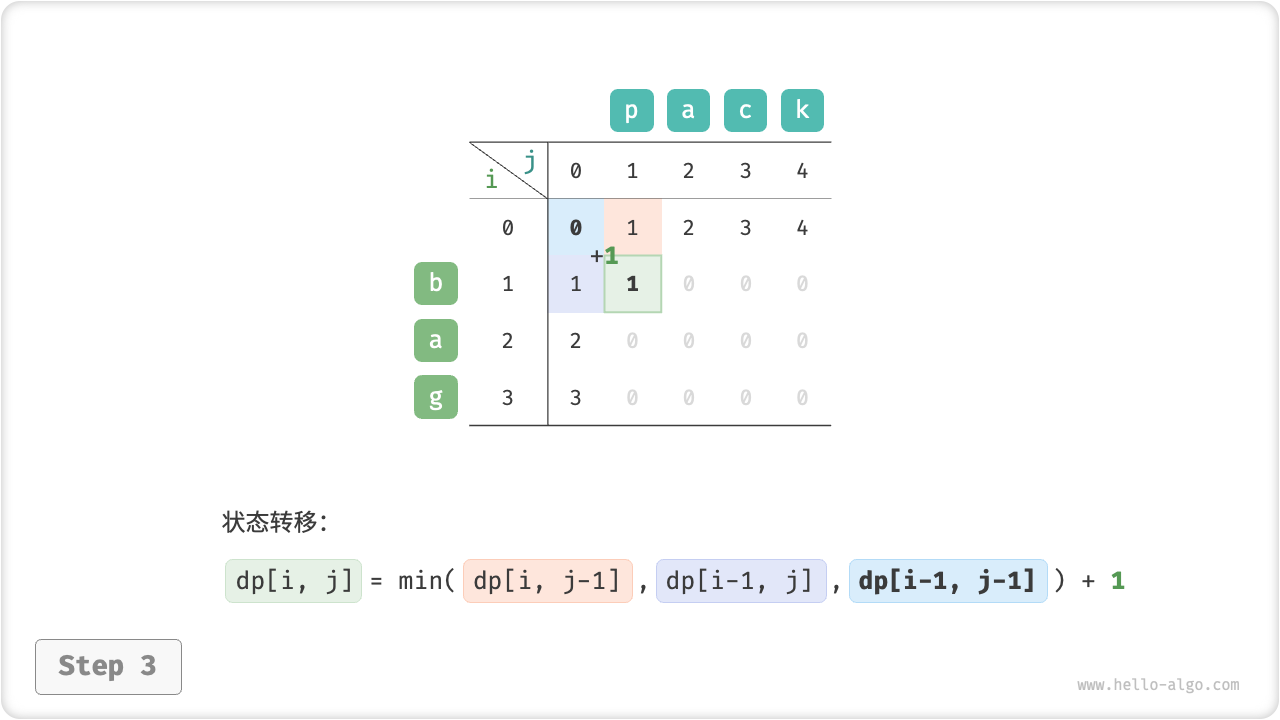
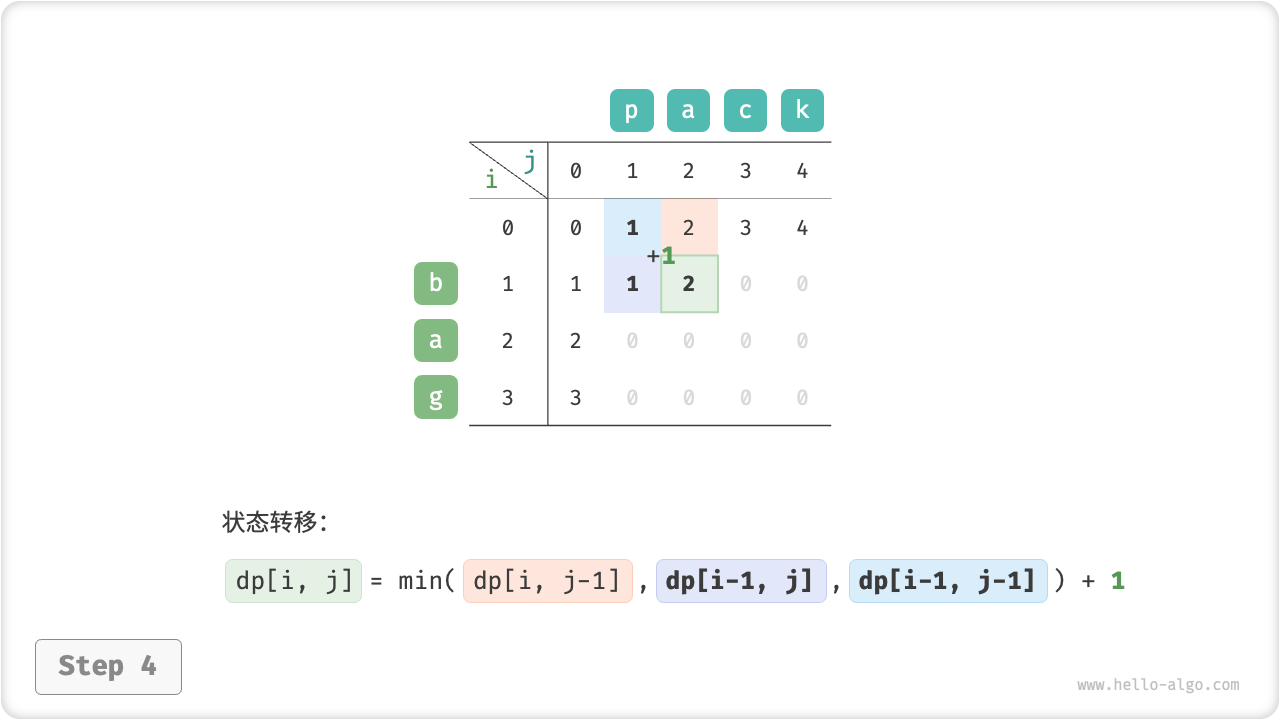
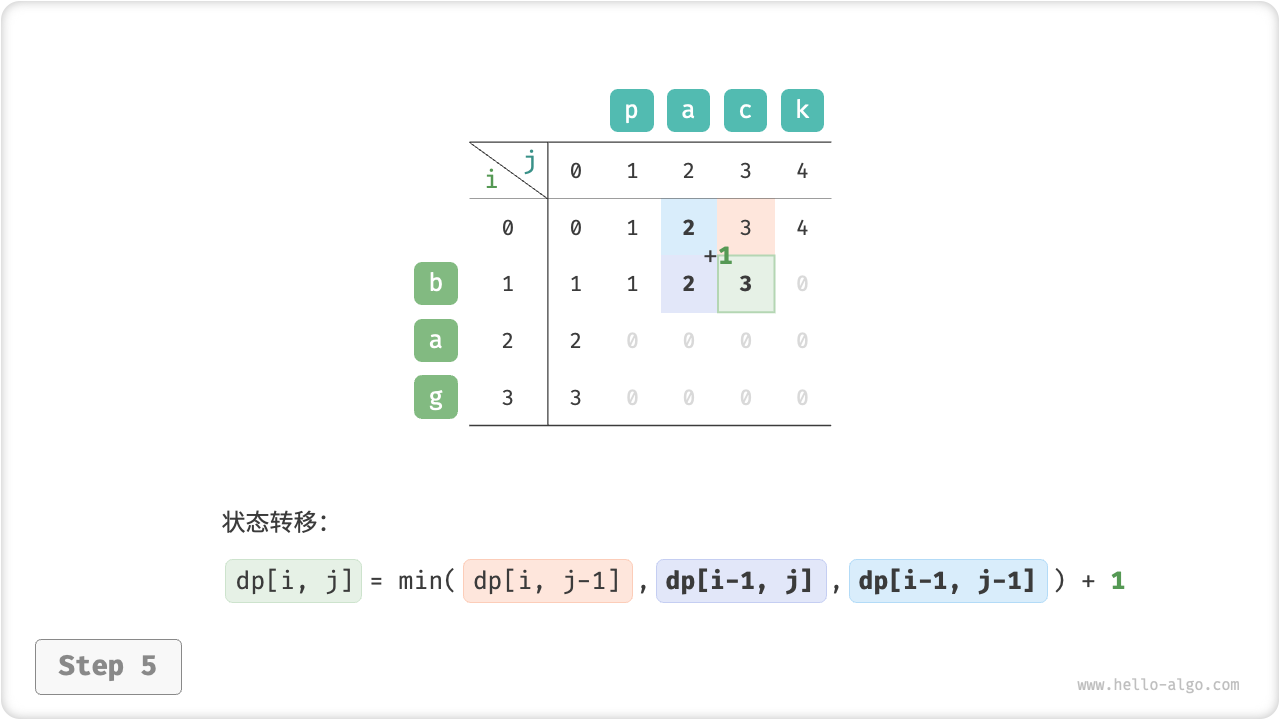
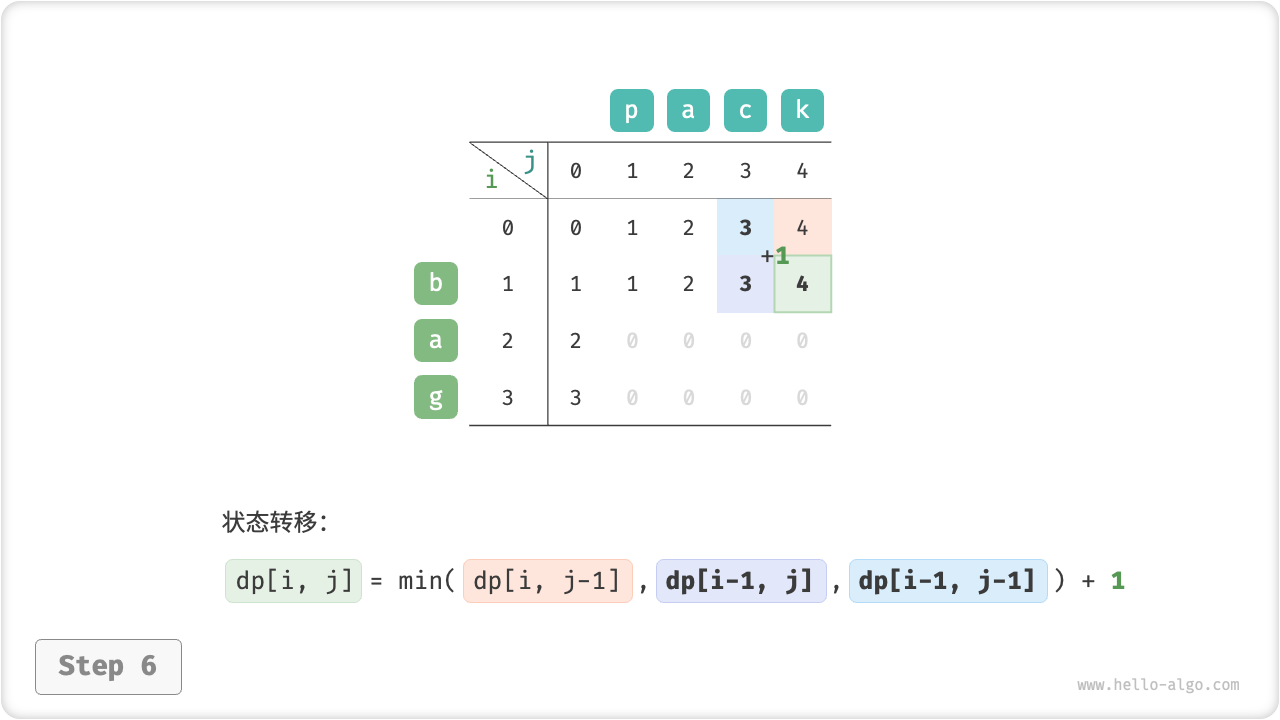
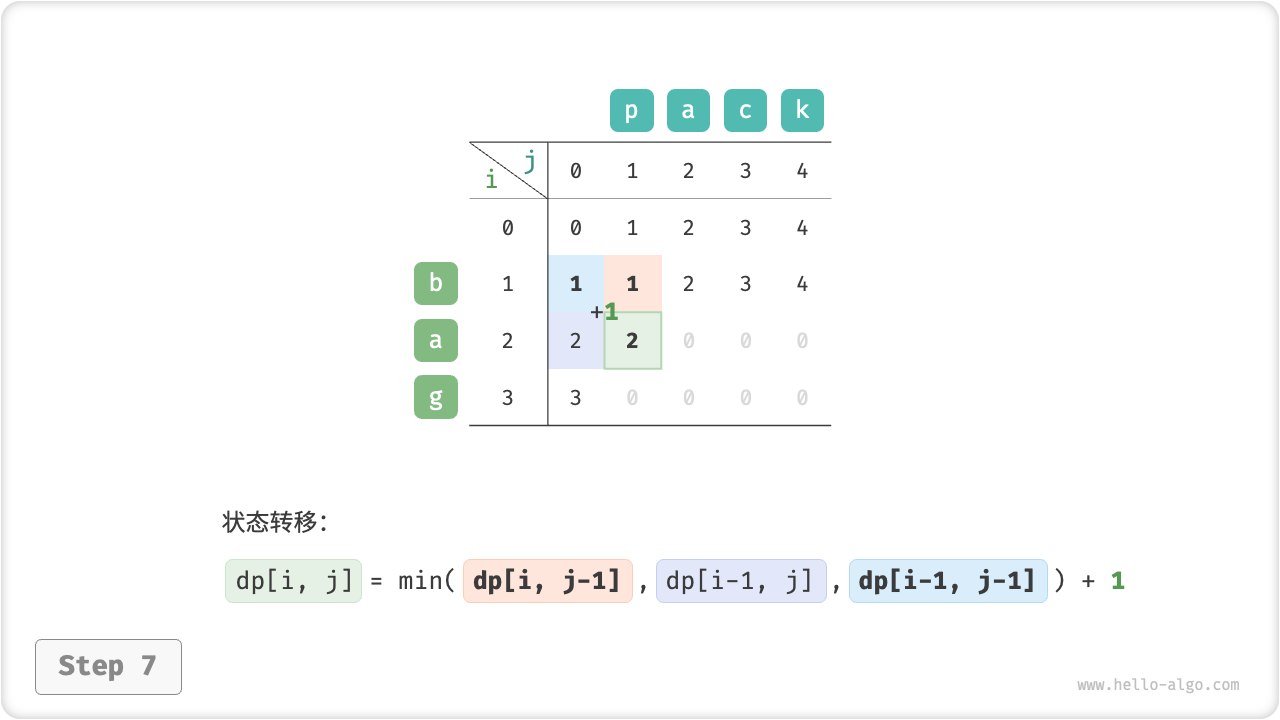
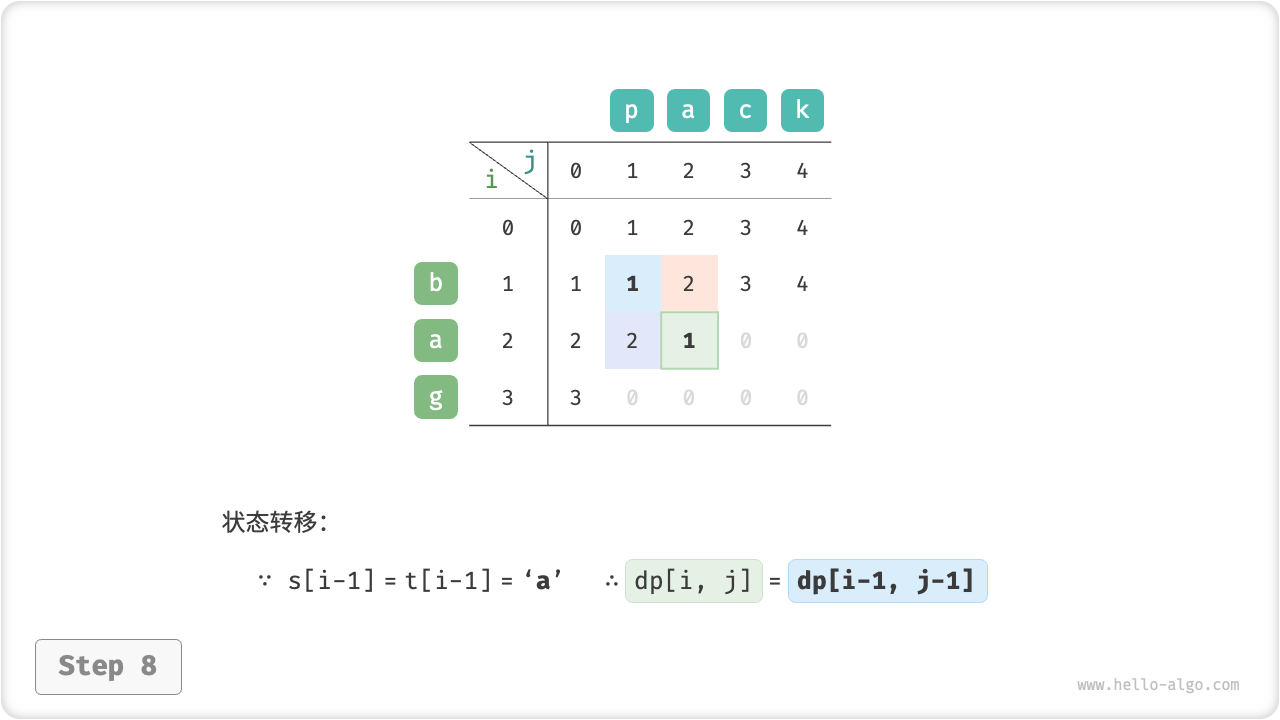
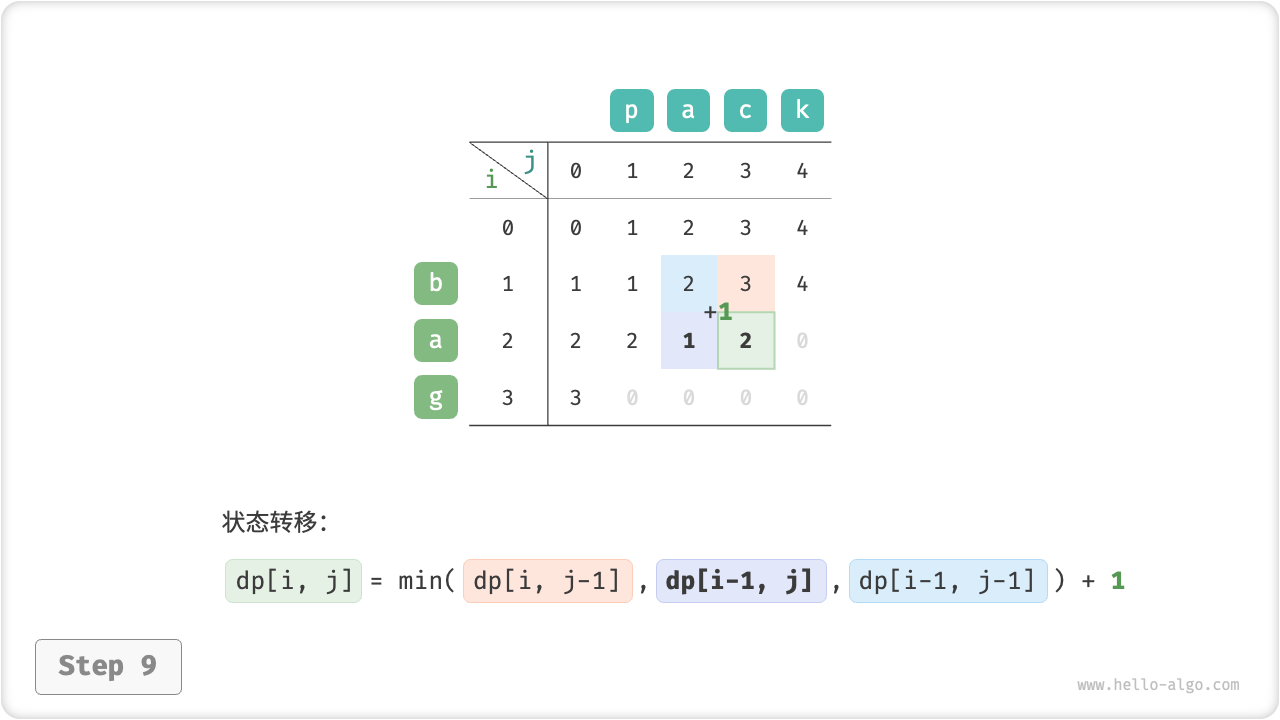
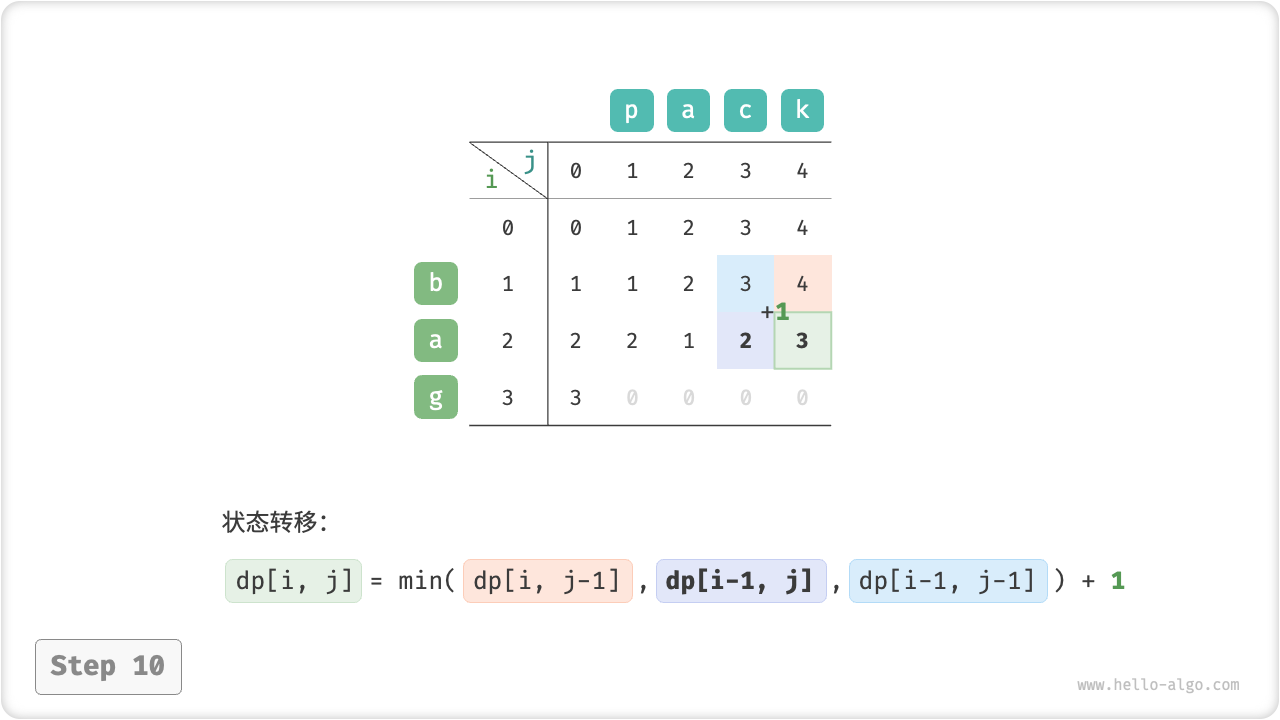
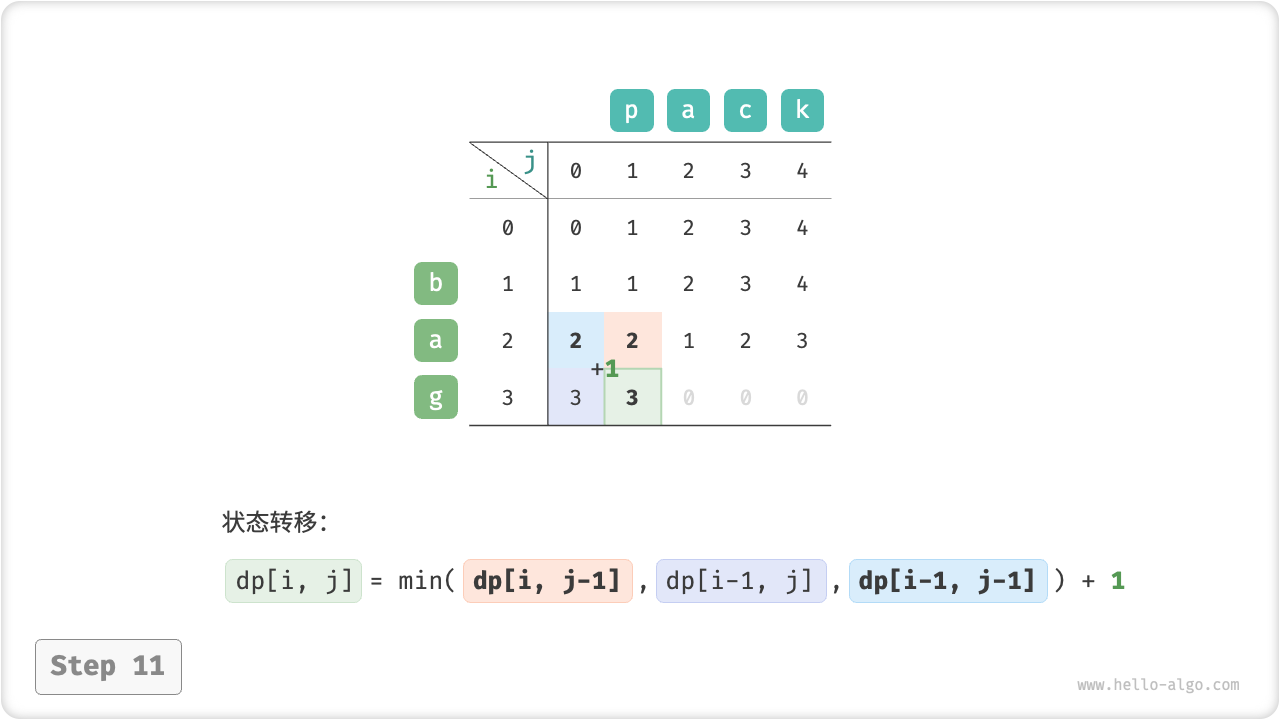
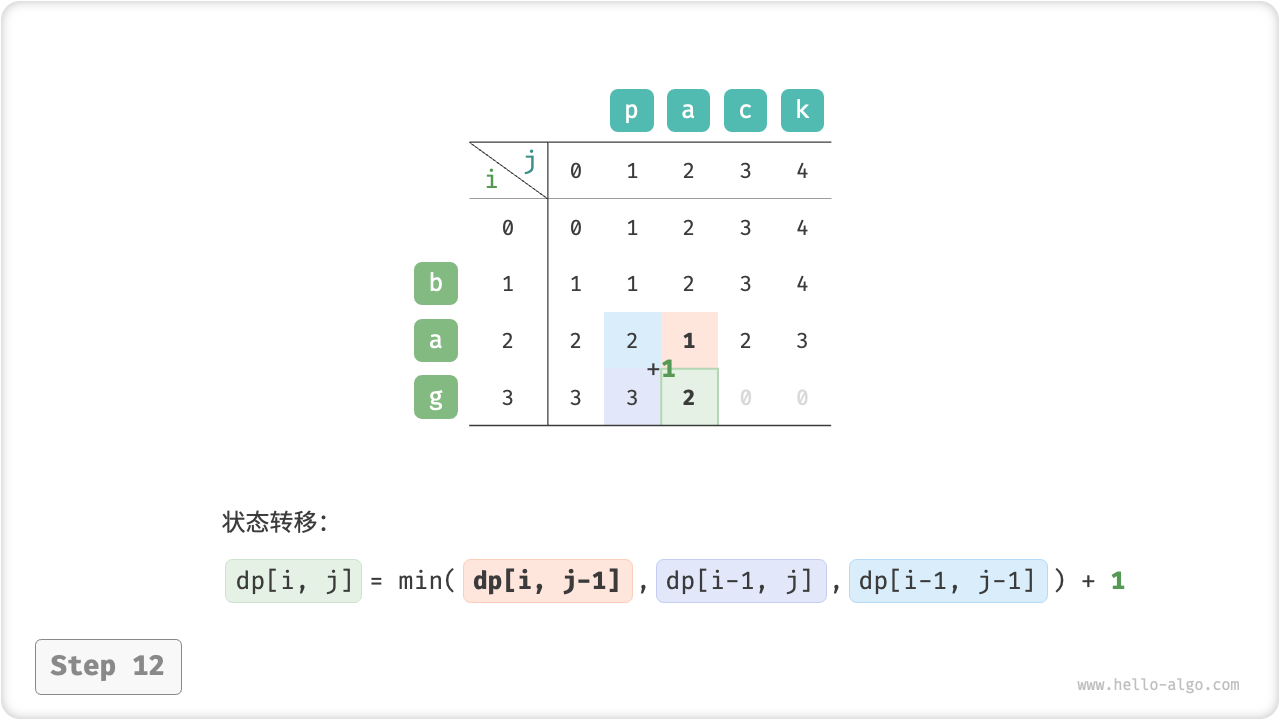
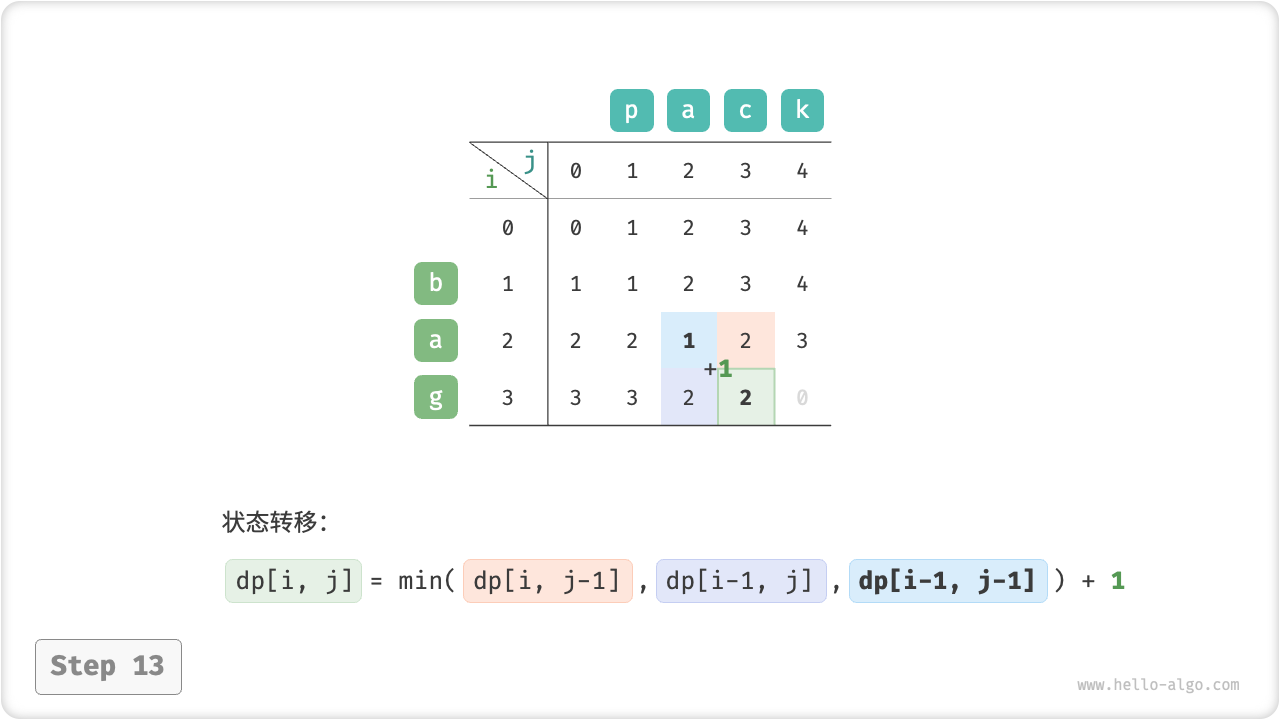
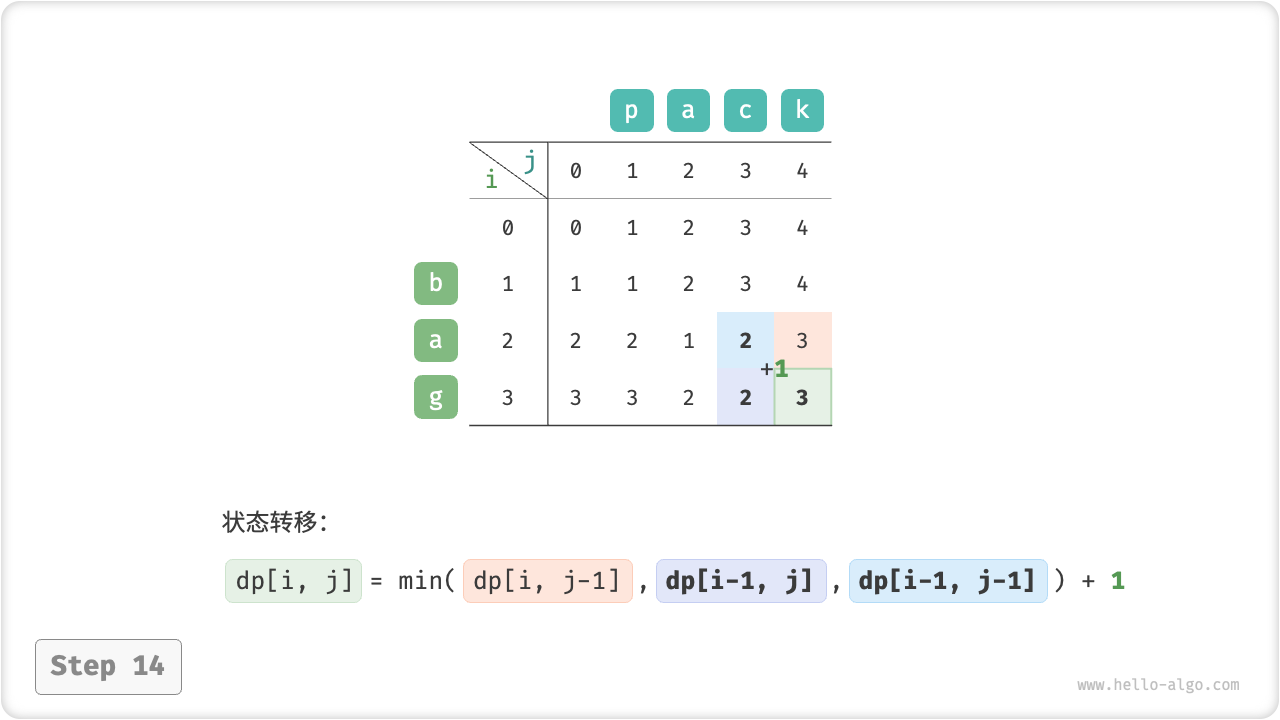
图 14-30   编辑距离的动态规划过程

3.   空间优化

由于 $dp[i,j]$ 是由上方 $dp[i-1,j]$、左方 $dp[i,j-1]$、左上方状态 $dp[i-1,j-1]$ 转移而来，而正序遍历会丢失左上方 $dp[i-1,j-1]$ ，倒序遍历无法提前构建 $dp[i,j-1]$ ，因此两种遍历顺序都不可取。

为此，我们可以使用一个变量 leftup 来暂存左上方的解 $dp[i-1,j-1]$ ，从而只需考虑左方和上方的解。此时的情况与完全背包问题相同，可使用正序遍历。

edit_distance.cpp

/* 编辑距离：空间优化后的动态规划 */
int editDistanceDPComp(string s, string t) {
    int n = s.length(), m = t.length();
    vector<int> dp(m + 1, 0);
    // 状态转移：首行
    for (int j = 1; j <= m; j++) {
        dp[j] = j;
    }
    // 状态转移：其余行
    for (int i = 1; i <= n; i++) {
        // 状态转移：首列
        int leftup = dp[0]; // 暂存 dp[i-1, j-1]
        dp[0] = i;
        // 状态转移：其余列
        for (int j = 1; j <= m; j++) {
            int temp = dp[j];
            if (s[i - 1] == t[j - 1]) {
                // 若两字符相等，则直接跳过此两字符
                dp[j] = leftup;
            } else {
                // 最少编辑步数 = 插入、删除、替换这三种操作的最少编辑步数 + 1
                dp[j] = min(min(dp[j - 1], dp[j]), leftup) + 1;
            }
            leftup = temp; // 更新为下一轮的 dp[i-1, j-1]
        }
    }
    return dp[m];
}