Assembly 整形表示法
2018-10-26 13:47 更新
整形有两种类型:有符号和无符号。无符号整形(即此类型没有负数)以一种非常直接的二进制方式来表示。数字200作为一个无符号整形数将被表示为11001000(或十六进制C8)。
1. 找到该数的反码
2. 将第一步的结果加1
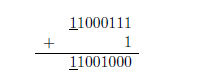


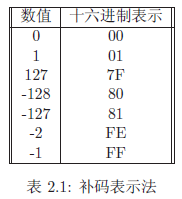
使用补码表示法,一个有符号的字节可以用来代表从¡128 到+127的数值。表2.1 展示一些可选的值。如果使用了16位,那么可以表示从¡32; 768到+32; 767的有符号数值。+32; 767可以表示为7FFF,¡32; 768 为8000, -128为FF80而-1为FFFF。32位的补码大约可以表示¡20亿到+20亿的数值范围。
CPU对某一的字节(或字,双字)具体表示多少并不是很清楚。汇编语言并没有类型的概念,而高级语言有。数据解释成什么取决于使用在这个数据上的指令。到底十六进制数FF被看成一个有符号数¡1 还是无符号数+255取决于程序员。C语言定义了有符号和无符号整形。这就使C编译器能决定使用正确的指令来使用数据。
有符号整形(即此类型可能为正数也可能为负数)以一种更复杂的方式来表示。例如,考虑¡56。+56当作一个字节来考虑时将被表示为00111000。在纸上,你可以将¡56表示为¡111000,但是在电脑内存中如何以一个字节来表示,如何储存这个负号呢?
有三种普遍的技术被用来在电脑内存中表示有符号整形。所有的方法都把整形的最大有效位当作一个符号位来使用。如果数为正数,则这一位为0;为负数,这一位就为1。
原码
第一种方法是最简单的,它被称为原码。它用两部分来表示一个整形。第一部分是符号位,第二部分是整形的原码。所以56表示成字节形式为00111000 (符号位加了下划线)而¡56将表示为10111000。
最大的一个字节的值将是01111111或+127,而最小的一个字节的值将是11111111或¡127。要得到一个数的相反数,只需要将符号位变反。这个方法很简单直接,但是它有它的缺点。首先,0会有两个可能的值:+0 (00000000) 和¡0(10000000)。因为0不是正数,也不是负数,所以这些表示法都应该把它表示成一样。这样会把CPU的运算逻辑弄得很复杂。第二,普通的运算同样是麻烦的。如果10加¡56,这个将改变为10减去56。同样,这将会复杂化CPU的逻辑。
反码
第二种方法称为反码表示法。一个数的反码可以通过将这个数的每一位求反得到。(另外一个得到的方法是:新的位值等于1¡老的位值。) 例如:00111000 (+56)的反码是11000111。在反码表示法中,计算一个数的反码等价于求反。因此,¡56就可以表示为11000111。注意,符号位在反码中
是自动改变的,你需要两次求反码来得到原始的数值。就像第一种方法一样,
是自动改变的,你需要两次求反码来得到原始的数值。就像第一种方法一样,
0有两种表示:
00000000 (+0)和11111111 (¡0)。
用反码表示的数值的运算同样是麻烦的。这有一个小诀窍来得到一个十六进制数值的反码,而不需要将它转换成二进制。这个诀窍就是用F(或十进制中的15)减去每一个十六进制位。这个方法假定数中的每一位的数值是由4位二进制组成的。这有一个例子:+56 用十六进制表示为38。要得到反码,用F减去每一位,得到C7。这个结果是与上面的结果吻合的。
补码
前面描述的两个方法用在早期的电脑中。现代的电脑使用第三种方法称为补码表示法。一个数的补码可以由下面两步得到:
1. 找到该数的反码
2. 将第一步的结果加1
这有一个使用00111000 (56)的例子。首先,经计算得到反码:11000111 。
然后加1:
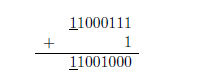
在补码表示法中,计算一个补码等价于对一个数求反。因此,11001000是¡56的补码。要得到原始数值需两次求反。令人惊讶的是补码不符合这个规定。通过对11001000的反码加1得到补码。

当在两个补码操作数间进行加法操作时,最左边的位相加可能会产生一个进位。这个进位是不被使用的。记住在电脑中的所有数据都是有固定大小的(根据位数多少)。两个字节相加通常得到一个字节的结果(就像两个字相加得到一个字,等。) 这个特性对于补码表示法来说是非常重要的。例如,把0作为一个字节来考虑它的补码形式(00000000)。计算它的补码形式得到总数:

其中c代表一个进位。(稍后将展示如何侦查到这个进位,但是它在这的结果中不储存。)因此,在补码表示法中0只有一种表示。这就使得补码的运算比前面的方法简单。
使用补码表示法,一个有符号的字节可以用来代表从¡128 到+127的数值。表2.1 展示一些可选的值。如果使用了16位,那么可以表示从¡32; 768到+32; 767的有符号数值。+32; 767可以表示为7FFF,¡32; 768 为8000, -128为FF80而-1为FFFF。32位的补码大约可以表示¡20亿到+20亿的数值范围。

CPU对某一的字节(或字,双字)具体表示多少并不是很清楚。汇编语言并没有类型的概念,而高级语言有。数据解释成什么取决于使用在这个数据上的指令。到底十六进制数FF被看成一个有符号数¡1 还是无符号数+255取决于程序员。C语言定义了有符号和无符号整形。这就使C编译器能决定使用正确的指令来使用数据。
以上内容是否对您有帮助:

 免费 AI IDE
免费 AI IDE



更多建议: