scikit-learn 聚类
可以使用模块 sklearn.cluster 对未标记的数据进行 聚类(Clustering) 。
每个聚类算法都有两个变体:一个是类,它实现了 fit 方法来学习训练数据上的簇,另一个是函数,给定训练数据,返回对应于不同簇的整数标签数组。对于类,可以在 labels_ 属性中找到训练数据上的标签。
输入数据
特别需要注意的一点是,本模块实现的算法可以采用不同类型的矩阵作为输入。所有算法的调用接口都接受 shape
[n_samples, n_features]的标准数据矩阵。 这些矩阵可以通过使用sklearn.feature_extraction模块中的类获得。对于AffinityPropagation,SpectralClustering和DBSCAN也可以输入 shape[n_samples, n_samples]的相似矩阵,可以通过sklearn.metrics.pairwise模块中的函数获得。
2.3.1. 聚类方法概述
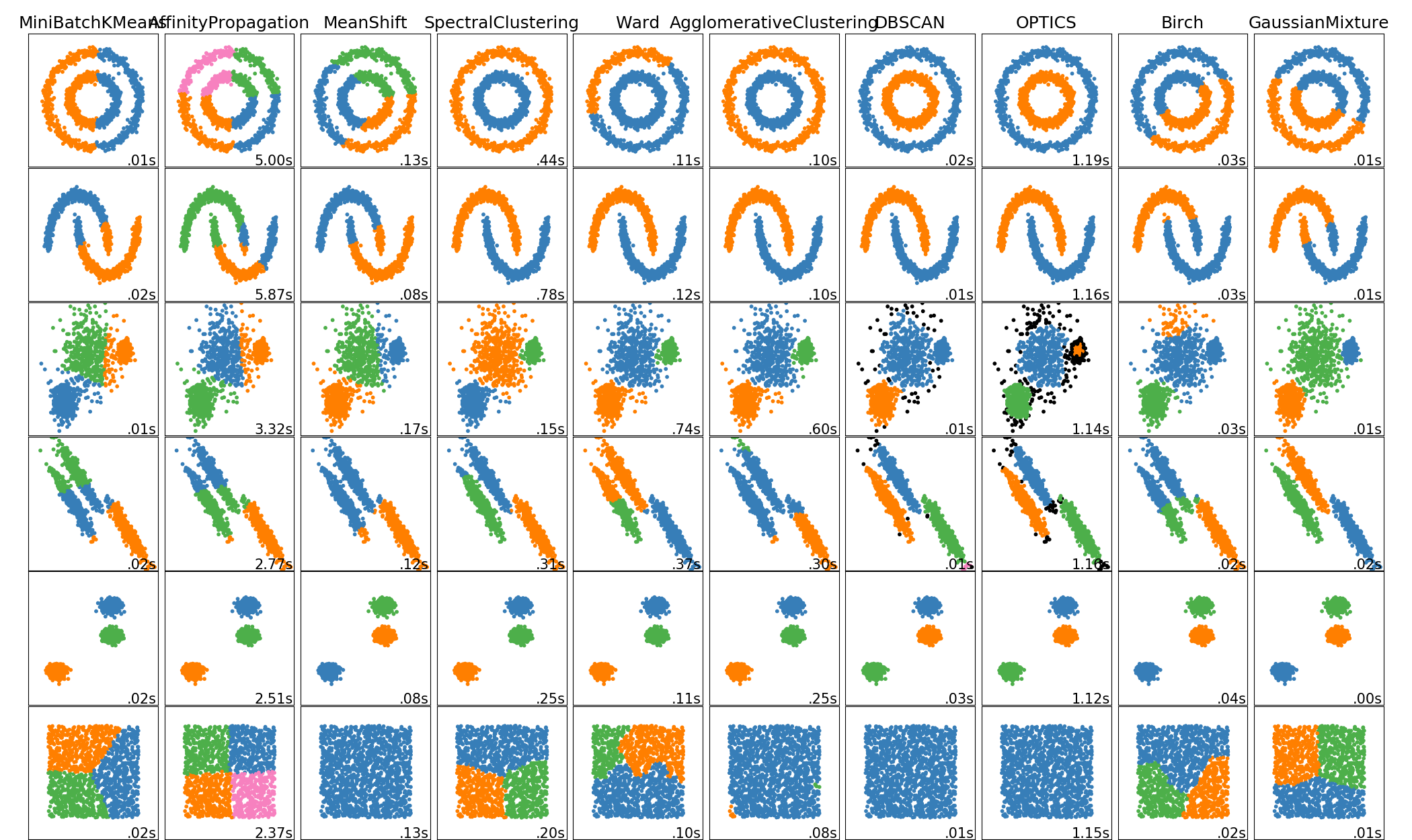
 scikit-learn 中聚类算法的比较
scikit-learn 中聚类算法的比较
| Method name(方法名称) | Parameters(参数) | Scalability(可扩展性) | Usecase(使用场景) | Geometry (metric used)(几何图形(公制)) |
|---|---|---|---|---|
| K-Means(K-均值) | number of clusters(聚类形成的簇的个数) | 非常大的 n_samples, 中等的 n_clusters 使用 MiniBatch 代码) |
通用, 均匀的 cluster size(簇大小), flat geometry(平面几何), 不是太多的 clusters(簇) | Distances between points(点之间的距离) |
| Affinity propagation | damping(阻尼), sample preference(样本偏好) | Not scalable with n_samples(n_samples 不可扩展) | Many clusters, uneven cluster size, non-flat geometry(许多簇,不均匀的簇大小,非平面几何) | Graph distance (e.g. nearest-neighbor graph)(图距离(例如,最近邻图)) |
| Mean-shift | bandwidth(带宽) | Not scalable with n_samples (n_samples不可扩展) |
Many clusters, uneven cluster size, non-flat geometry(许多簇,不均匀的簇大小,非平面几何) | Distances between points(点之间的距离) |
| Spectral clustering | number of clusters(簇的个数) | 中等的 n_samples, 小的 n_clusters |
Few clusters, even cluster size, non-flat geometry(几个簇,均匀的簇大小,非平面几何) | Graph distance (e.g. nearest-neighbor graph)(图距离(例如最近邻图)) |
| Ward hierarchical clustering | number of clusters(簇的个数) | 大的 n_samples 和 n_clusters |
Many clusters, possibly connectivity constraints(很多的簇,可能连接限制) | Distances between points(点之间的距离) |
| Agglomerative clustering | number of clusters(簇的个数), linkage type(链接类型), distance(距离) | 大的 n_samples 和 n_clusters |
Many clusters, possibly connectivity constraints, non Euclidean distances(很多簇,可能连接限制,非欧氏距离) | Any pairwise distance(任意成对距离) |
| DBSCAN | neighborhood size(neighborhood 的大小) | 非常大的 n_samples, 中等的 n_clusters |
Non-flat geometry, uneven cluster sizes(非平面几何,不均匀的簇大小) | Distances between nearest points(最近点之间的距离) |
| Gaussian mixtures(高斯混合) | many(很多) | Not scalable(不可扩展) | Flat geometry, good for density estimation(平面几何,适用于密度估计) | Mahalanobis distances to centers( 与中心的马氏距离) |
| Birch | branching factor(分支因子), threshold(阈值), optional global clusterer(可选全局簇). | 大的 n_clusters 和 n_samples |
Large dataset, outlier removal, data reduction.(大型数据集,异常值去除,数据简化) |
当簇具有一个特定的形状,即非平面流体,并且标准欧氏距离不是正确的度量标准时,非平面几何聚类是非常有用的。这种情况出现在上图的前两行中。
用于聚类(clustering)的高斯混合模型,将在文档的另一章描述混合模型。KMeans可以看作是每个分量协方差相等的高斯混合模型的一个特例。
2.3.2. K-means
KMeans 算法通过把样本分离成 n 个具有相同方差的类的方式来对数据进行聚类,最小化一个称为惯量或簇内平方和的准则(见下文)。该算法需要指定簇的数量。它可以很好地扩展到大量样本,并已经在许多不同领域的应用领域被广泛使用。
k-means 算法将一组 样本 划分成 个不相交的簇 ,每个都用该簇中样本的均值 描述。 这个均值通常被称为簇的 “质心”; 尽管它们处在同一个空间,但它们通常不是从 中挑选出的点,虽然它们是处在同一个空间。
K-means算法旨在选择一个质心, 能够最小化惯性或簇内平方和的标准:
$$\sum_{i=0}^{n} \min {\mu{j} \in C}\left(\left|x_{i}-\mu_{j}\right|^{2}\right)$$
惯性被认为是测量簇内聚程度的尺度。它有很多缺点:
惯性假设簇是凸的,各项同性的,但并不总是这样。它对细长的簇或具有不规则形状的流形反应很差。 惯性不是一个归一化度量: 我们只知道当惯量的值越低越好,零是最优的。但是在非常高维的空间中,欧氏距离往往会膨胀(这就是所谓的 “”的一个例子)。在 k-means 聚类算法之前运行主成分分析(PCA)等降维算法可以缓解这个问题并加快计算速度。

K-means 通常被称为 Lloyd 算法。简单来说,算法有三个步骤。第一步是选择初始质心,最基本的方法是从数据集中选择个样本。初始化之后,K-means由其他两个步骤之间的循环组成。第一步将每个样本分配到其最近的质心。第二步是通过取分配给前一个质心的所有样本的平均值来创建新的质心。计算新旧质心之间的差值,算法重复最后两个步骤,直到该值小于阈值。换句话说,算法重复这个步骤,直到质心不再明显移动。
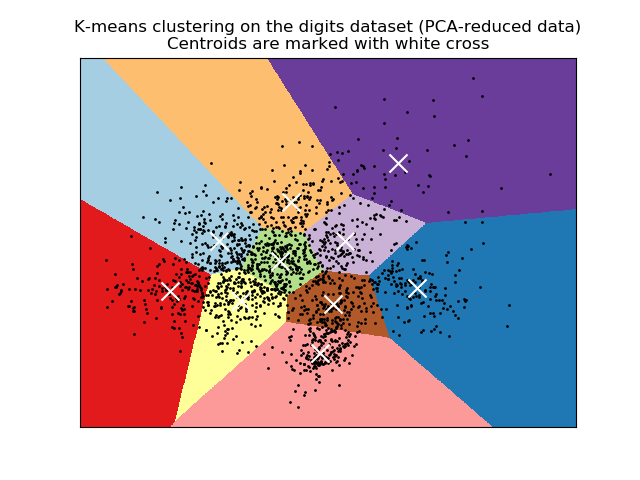
 K-means 相当于一个具有小的、完全相等的、对角协方差矩阵的期望最大化算法。
K-means 相当于一个具有小的、完全相等的、对角协方差矩阵的期望最大化算法。
算法也可以通过 Voronoi diagrams(voronoi图)的概念来理解。首先,使用当前质心计算点的Voronoi图。Voronoi图中的每个段成为一个单独的簇。其次,将质心更新为每个段的平均值。然后算法重复这个过程,直到满足停止条件。通常,当迭代之间目标函数的相对下降量小于给定的公差值时,算法停止。在此实现中不是这样的:当质心移动小于公差时迭代停止。
只要有足够的时间,K-means 将总是收敛的,但这可能是局部的最小值。这很大程度上取决于质心的初始化。 因此,初始化不同质心的计算通常会进行几次。帮助解决这个问题的一种方法是 k-means++ 初始化方案,它已经在 scikit-learn 中实现(使用 init='k-means++' 参数)。 这将初始化质心(通常)彼此远离,相对随机初始化得到更好的结果,如参考文献所示。
该算法支持样本权重功能,样本权重可以由参数sample_weight给出。该功能允许计算簇中心和惯性值时为一些样本分配更多的权重。 例如,给某个样本分配一个权重值2,相当于在数据集X中增加一个该样本的重复项。
K-means可用于矢量量化。这是利用 KMeans 训练模型的变换方法实现的。
2.3.2.1. 低级并行
KMeans通过Cython从基于OpenMP的并行性中获益。并行处理小块数据(256个样本),这还会产生较低的内存占用。有关如何控制线程数量的详细信息,请参阅我们的Parallelism说明。
示例:
k-均值假设的证明: 演示 k-means 是否直观地执行,何时不执行 手写数字数据的K-Means聚类演示: 聚类手写数字
参考资料:
“k-means++: The advantages of careful seeding” Arthur, David, and Sergei Vassilvitskii, Proceedings of the eighteenth annual ACM-SIAM symposium on Discrete algorithms, Society for Industrial and Applied Mathematics (2007)
2.3.2.2. 小批量 K-Means
MiniBatchKMeans 是 KMeans 算法的变体,它使用小批量(mini-batches)来减少计算时间,同时仍然试图优化相同的目标函数。小批量是输入数据的子集,在每次训练迭代中随机抽样。这些小批量极大减少了收敛到局部解所需的计算量。 与其他降低 k-means 收敛时间的算法相比,小批量 k-means 产生的结果一般只比标准算法略差。
算法在两个主要步骤之间迭代,类似于普通的k-means。在第一步中,从数据集中随机抽取样本,以形成一个小批量。然后把它们分配给最近的质心。在第二步,质心被更新。与k-means相比,这是在每个样本的基础上完成的。对于小批量的每个样本,将通过对样本和之前分配给该样本的所有样本的流平均值更新分配的质心。这具有随时间减少质心变化率的效果。这些步骤一直执行到收敛或达到预定的迭代次数。
MiniBatchKMeans 收敛速度比 KMeans快 ,但是结果的质量会降低。在实践中,质量差异可能非常小,如示例和引用的参考文献所示。
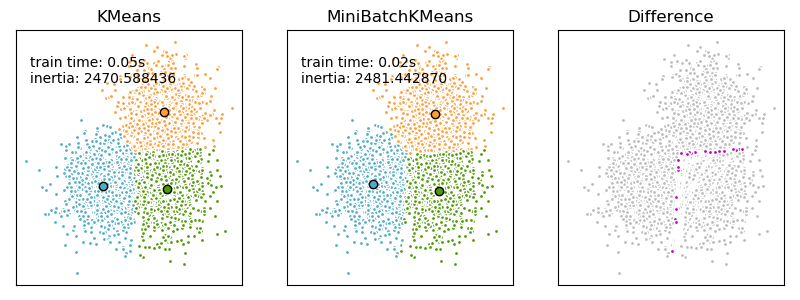
 示例:
示例:
K-Means和MiniBatchKMeans聚类算法的比较: KMeans与MiniBatchKMeans的比较 基于k-means的文本文档聚类: 使用稀疏MinibtchKMeans进行文档聚类 人脸的部分词典的在线学习
参考文献:
“Web Scale K-Means clustering” D. Sculley, Proceedings of the 19th international conference on World wide web (2010)
2.3.3. Affinity Propagation
AffinityPropagation AP聚类是通过在样本对之间发送消息直到收敛的方式来创建聚类。然后使用少量有代表性的样本作为聚类中心来描述数据集,而这些样本对可以被认为是最能代表数据集中其它数据的样本。把样本对之间发送的消息作为一个样本对另一个样本的模范样本的适合程度,适合程度值在根据来自其他对的值不断更新。这种更新以迭代的方式进行,直到收敛为止,此时会选择最终的范例,从而给出最终的聚类。
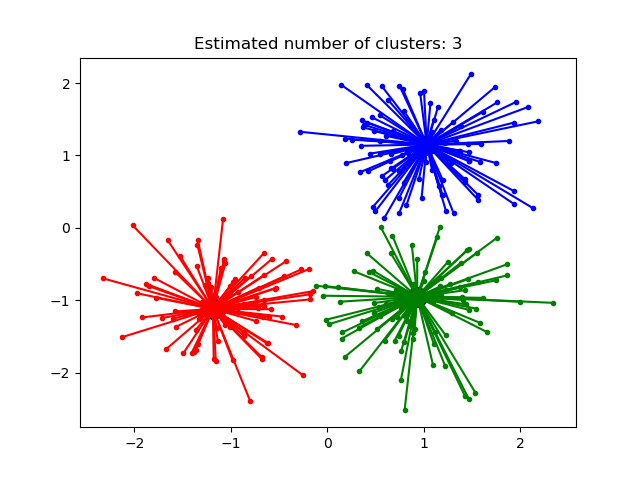
 Affinity Propagation 算法非常有趣,因为它可以根据提供的数据决定聚类的数量。 因此有两个比较重要的参数是preference(控制使用多少模范样本 )和阻尼因子(damping factor) 减少吸引信息和归属信息以避免更新信息时的数据振荡。
Affinity Propagation 算法非常有趣,因为它可以根据提供的数据决定聚类的数量。 因此有两个比较重要的参数是preference(控制使用多少模范样本 )和阻尼因子(damping factor) 减少吸引信息和归属信息以避免更新信息时的数据振荡。
AP聚类算法主要的缺点是它的复杂度。Affinity Propagation 聚类算法的时间复杂度是 , 其中是样本的个数 ,是收敛前迭代的次数。如果使用密集相似矩阵,其空间复杂度是。但如果使用稀疏相似性矩阵可以降低空间复杂度。 这使得Affinity Propagation 算法最适合中小型数据集。
示例:
亲和传播聚类算法演示: 三类合成二维数据集上的亲和传播。 股票市场结构的可视化 金融时间序列的亲和传播寻找组
Algorithm description(算法描述): 样本之间传递的信息有两种。 第一种是吸引信息 (responsibility) , 样本 适合作为样本 的聚类中心的程度。第二种是归属信息(availability) , 的合适程度。 这样,选取示例样本作为聚类中心, 如果 (1) 该样本与其许多样本相似,并且 (2) 被许多样本选择可以代表他们自己,样本就会被选择。
样本对样本吸引度计算公式为:
其中 是样本 和样本 之间的相似度。样本 作为样本 的示例样本的合适程度:
算法开始时 和 都被置 0,然后开始迭代计算直到收敛。 为了防止更新数据时出现数据振荡,在迭代过程中引入阻尼因子 :
其中 是迭代的次数。
2.3.4. Mean Shift
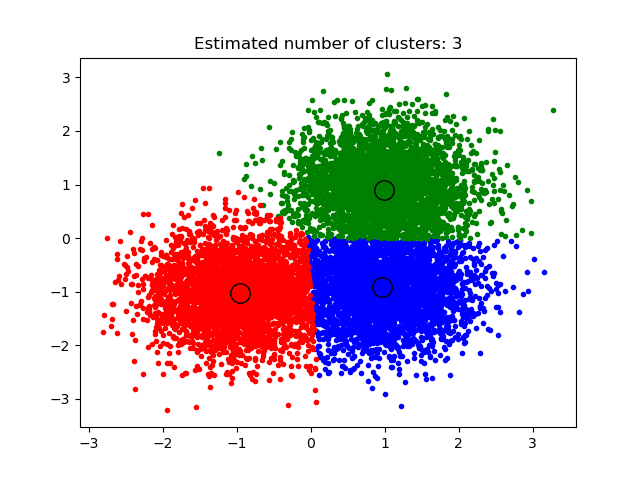
MeanShift 算法目的是在一个平滑的样本密度中返现 blobs 。它是一种基于质心的算法,其工作原理是将候选质心的位置更新为给定区域内点的平均值。然后在后处理阶段对这些候选质心位置进行筛选,以消除近似重复,形成最终的质心集合。
给定第次迭代中的候选质心 , 候选质心的位置按照如下公式更新:
其中 是围绕 周围一个给定距离范围内的样本邻域, 是均值偏移向量(mean shift vector), 该向量是所有质心中指向点密度增加最多的区域的偏移向量。使用以下等式计算,有效地将质心更新为其邻域内样本的平均值:
该算法自动设置簇的数量,而不是依赖参数bandwidth指示要搜索的区域大小的参数。该参数可以手动设置,但如果未设置带宽,可以使用提供的estimate_bandwidth函数进行估算 。
该算法不是高度可扩展的,因为在执行该算法时需要进行多个最近邻搜索。该算法保证收敛,但是当质心的变化较小时,该算法将停止迭代。
通过找到给定样本的最近质心来标记新样本。
 示例:
示例:
mean-shift聚类算法的演示: 三类合成二维数据集的Mean-Shift聚类。
参考文献:
“Mean shift: A robust approach toward feature space analysis.” D. Comaniciu and P. Meer, IEEE Transactions on Pattern Analysis and Machine Intelligence (2002)
2.3.5. Spectral clustering(谱聚类)
SpectralClustering对样本之间的关联矩阵执行低维嵌入,然后在低维空间中对特征向量的分量进行聚类(例如,通过K-Means聚类)。amg求解器用于特征值问题,如果关联矩阵是稀疏的,那么在计算效率会很高。(请注意,amg求解器需要安装pyamg模块。)
当前版本的SpectralClustering需要预先指定簇的数量。它适用于簇数量少时,簇数量多时不建议使用。
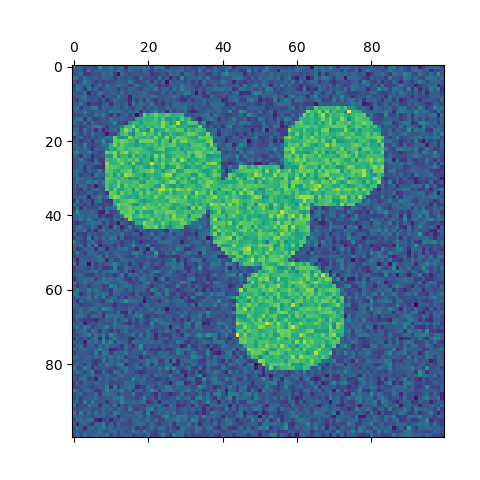
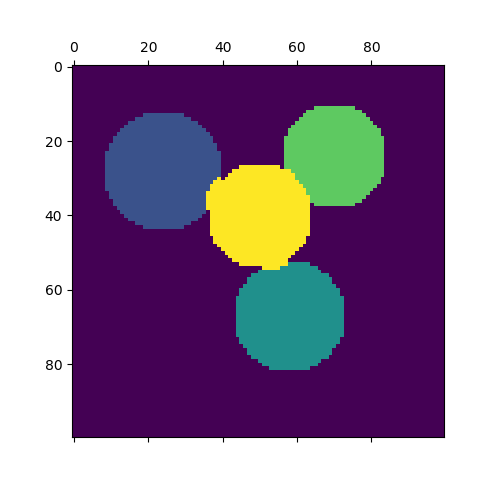
对于两个簇,SpectralClustering解决了相似性图形上归一化切割问题的凸松弛问题:将图形切割成两半,以使所切边缘的权重比每个簇内边缘的权重小。此标准特别有趣:当处理图形的顶点为像素,相似图形的边缘是图像的渐变函数。

 警告:将距离转换为行为良好的相似性
警告:将距离转换为行为良好的相似性
请注意,如果相似性矩阵的值分布不均,例如具有负值或距离矩阵并不表示相似性,则 spectral problem 问题将变成奇异的,并且无法解决。在这种情况下,建议对矩阵的 entries 进行转换。例如,在有向距离矩阵上应用heat kernel:
similarity = np.exp(-beta * distance / distance.std())
请参阅此类应用程序的示例。
示例: 光谱聚类在图像分割中的应用: 利用谱聚类从噪声背景中分割目标。 分割区域中希腊硬币的图片: 光谱聚类以分割区域中硬币的图像。
2.3.5.1. 不同的标签分配策略
SpectralClustering对应的assign_labels参数,可以使用不同的标签分配策略。 "kmeans"可以匹配更详细的数据信息,但可能不稳定。特别是,除非你可以控制random_state,否则它可能无法复现运行的结果,因为它取决于随机初始化。使用"discretize"策略是100%可复现的,但往往会创建几何形状相当均匀的闭合包。


2.3.5.2. 谱聚类图表
谱聚类还可用于通过其频谱嵌入对图形进行分区。在这种情况下,亲和度矩阵是图的邻接矩阵,并且SpectralClustering可以由affinity='precomputed'进行初始化:
>>> from sklearn.cluster import SpectralClustering
>>> sc = SpectralClustering(3, affinity='precomputed', n_init=100,
... assign_labels='discretize')
>>> sc.fit_predict(adjacency_matrix)
参考文献:
“A Tutorial on Spectral Clustering” Ulrike von Luxburg, 2007 “Normalized cuts and image segmentation” Jianbo Shi, Jitendra Malik, 2000 “A Random Walks View of Spectral Segmentation” Marina Meila, Jianbo Shi, 2001 “On Spectral Clustering: Analysis and an algorithm” Andrew Y. Ng, Michael I. Jordan, Yair Weiss, 2001 “Preconditioned Spectral Clustering for Stochastic Block Partition Streaming Graph Challenge” David Zhuzhunashvili, Andrew Knyazev
2.3.6. 层次聚类
层次聚类是一种通过连续合并或拆分内置聚类来构建最终聚类的聚类算法。聚类的层次结构表示为树(或树形图)。树的根是所有的样本中唯一的聚类,叶子是只有一个样本的集群。有关更多详细信息,请参见Wikipedia页面。
AgglomerativeClustering使用自下而上的方法执行层次聚类:每个观察都从其自己的聚类开始,并且聚类连续合并在一起。连接标准确定用于合并策略的度量标准:
Ward最小化了所有群集内的平方差总和。这是方差最小化的优化方法,从这个意义上讲,它类似于k均值目标函数的优化方法,但采用了凝聚分层的方法。 Maximum 或 complete linkage 最小化成对聚类间最远样本的距离。 Average linkage 最小化成对聚类间平均样本的距离值。 Single linkage 最小化成对聚类间最近样本的距离值。
AgglomerativeClustering 在联合使用同一个连接矩阵时,也可以扩大到大量样本,但是在样本之间没有添加连接约束时,在计算上代价很大:在每一步都要考虑所有可能的合并。
FeatureAgglomeration使用凝聚聚类将看上去相似的特征组合在一起,从而减少特征的数量。它是一个降维工具, 请参阅 无监督降维。
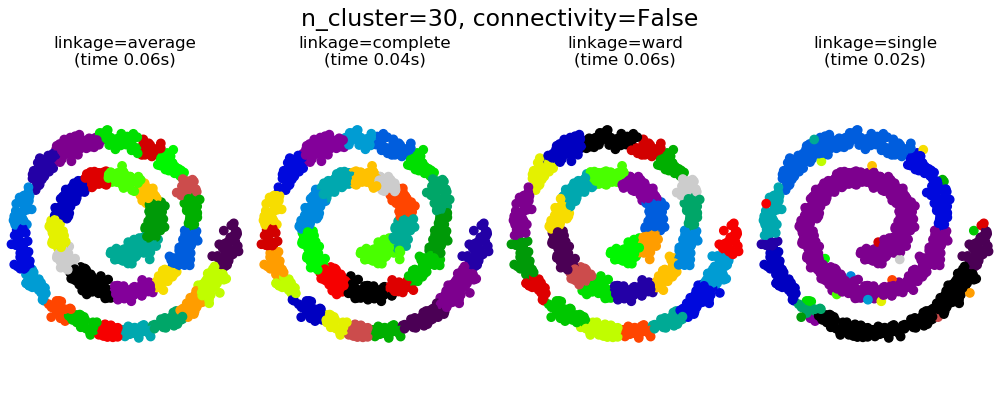
2.3.6.1. 不同连接类型: Ward, complete,average and single linkage
AgglomerativeClustering 支持Ward,single, average, 和 complete linkage 策略。
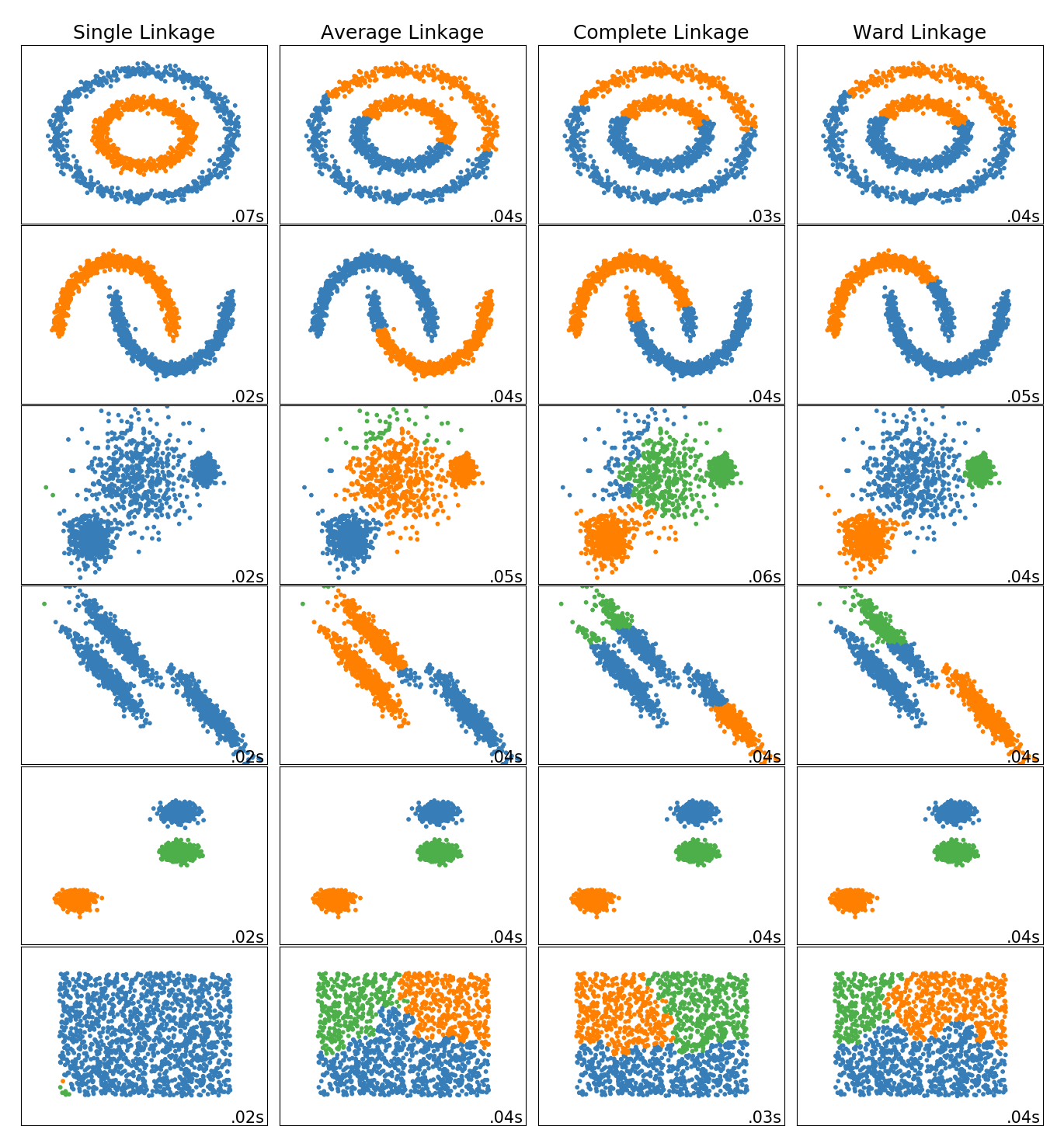
 Agglomerative cluster 存在 “rich get richer” 现象,导致聚类大小不均匀。在这方面,Single linkage 是最差的策略,而Ward给出的规则大小最大。但是, affinity (或聚类中使用的距离)不能随Ward一起变化,因此对于非欧氏度量,average linkage 是一个很好的选择。average linkage虽然对嘈杂的数据的鲁棒性并不强,但是对规模较大的数据集提供了非常有效的层次聚类算法。 Single linkage 同样对非全局数据有很好的效果。
Agglomerative cluster 存在 “rich get richer” 现象,导致聚类大小不均匀。在这方面,Single linkage 是最差的策略,而Ward给出的规则大小最大。但是, affinity (或聚类中使用的距离)不能随Ward一起变化,因此对于非欧氏度量,average linkage 是一个很好的选择。average linkage虽然对嘈杂的数据的鲁棒性并不强,但是对规模较大的数据集提供了非常有效的层次聚类算法。 Single linkage 同样对非全局数据有很好的效果。
示例:
Various Agglomerative Clustering on a 2D embedding of digits: exploration of the different linkage strategies in a real dataset.
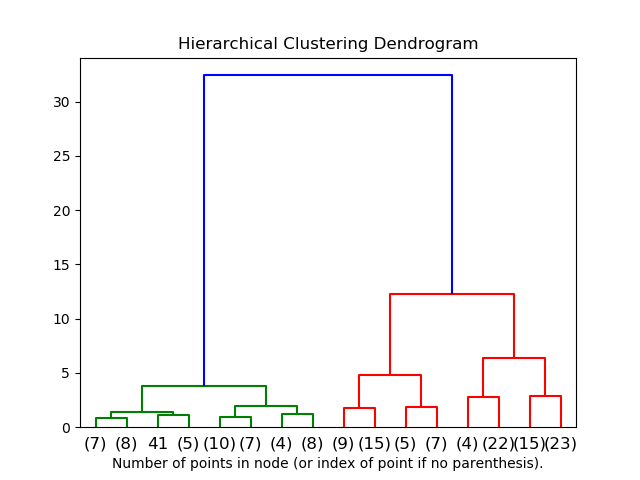
2.3.6.2. 聚类分层结构可视化
可以将表示聚类层次合并的树可视化为树状图。视觉检查通常有助于理解数据的结构,在小样本情况下更是如此。

2.3.6.3. 添加连接约束
AgglomerativeClustering的一个有趣的特点是可以通过一个连接矩阵将连接约束添加到该算法中(只能将相邻的聚类合并在一起),连接矩阵为每个样本定义了遵循给定数据结构的相邻样本。例如,在下面的swiss-roll示例中,连接约束禁止合并不相邻的 swiss roll ,从而避免形成在 roll 上折叠的簇。
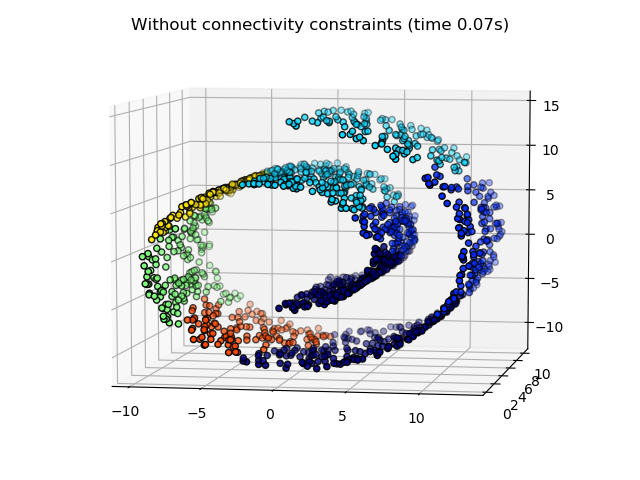
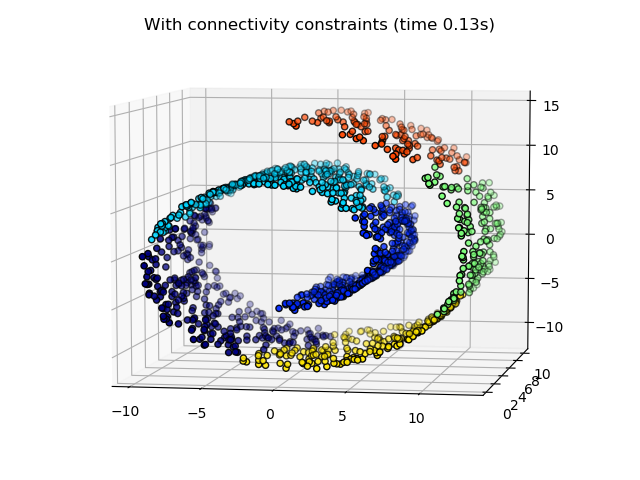


这些约束对于强加特定的局部结构是有用的,而且也使算法更快,特别是当样本数量很大的时候。
连通性约束是通过连通性矩阵施加的:一个稀疏矩阵,其仅在行和列的交点处具有要连接的数据集索引。该矩阵可以由先验信息构建:例如,您可能希望仅通过具有指向彼此的链接的合并页面来对web页面进行聚类。也可以从数据中得知,例如,sklearn.neighbors.kneighbors_graph,用于限制与最近邻的合并,如本例所示;或sklearn.feature_extraction.image.grid_to_graph,如coin示例中,用于仅允许合并图像上的相邻像素 点。
示例:
基于硬币图像的结构化区域分层聚类演示: 沃德聚类在区域内分割硬币图像。 分层聚类:结构化区域与非结构化区域: 瑞士卷上的Ward算法示例,结构化方法与非结构化方法的比较。 特征聚集与单变量选择: 基于Ward层次聚类的特征聚集降维实例。 带结构和无结构的凝聚聚类
警告:single, average and complete linkage的连接约束
single, average and complete linkage的连接约束可以增强聚合聚类中的 ‘rich getting richer’ 现象,尤其是如果他们是用sklearn.neighbors.kneighbors_graph来构建时。在少数簇的限制下,它们倾向于给出一些宏观上占据的簇,并且几乎是空的簇。(请参阅带结构和无结构的凝聚聚类的讨论 )。就此问题而言,single是最脆弱的linkage选项。







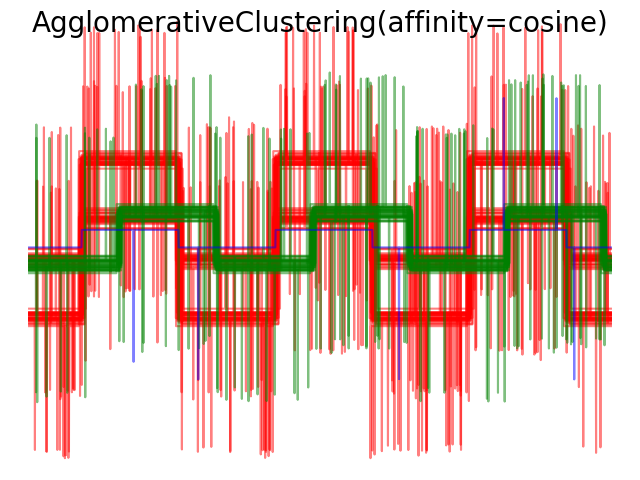
2.3.6.4. Varying the metric
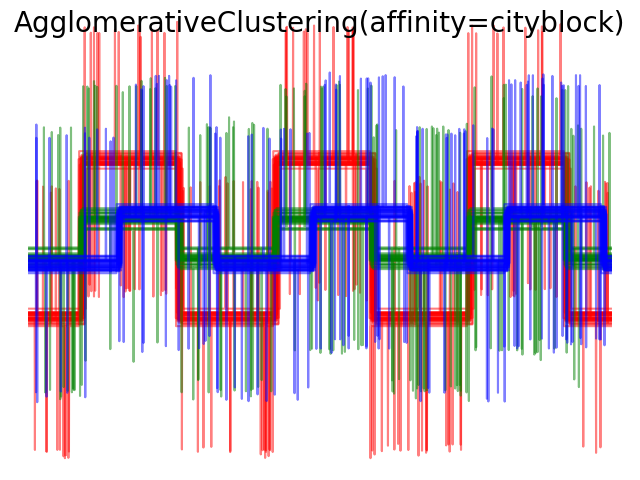
Single, verage and complete linkage 可以使用各种距离 (or affinities), 特别是欧氏距离 (l2), 曼哈顿距离(Manhattan distance)(or Cityblock, or l1), 余弦距离(cosine distance), 或者任何预先计算的关联矩阵(affinity matrix).
l1 距离有利于稀疏特征或者稀疏噪声: 例如很多特征都是0,就像在文本挖掘中使用出现的稀有单词一样。 余弦距离很有趣,因为它对信号的全局缩放是不变的。
选择度量标准的知道原则是使得不同类样本之间距离最大化,并且最小化同类样本之间的距离



 示例:
示例:
2.3.7. DBSCAN
该DBSCAN算法将簇视为低密度区域将高密度区域分隔开。由于这种相当通用的观点,DBSCAN发现的簇可以是任何形状,而k-均值假定簇是凸形的。DBSCAN的核心组件是core samples,即高密度区域中的样本。因此,一个簇是一组核心样本,每个样本彼此接近(通过某种距离度量来衡量),以及一组与核心样本接近(但本身不是核心样本)的非核心样本。该算法有两个参数, min_samples和eps,它们正式定义了我们说稠密 (dense)时的含义。更高的min_samples或更低的eps 都表示形成簇所需的更高密度。
更正式地说,我们将核心样本定义为数据集中的一个样本的 eps 距离范围内的min_samples其他样本,以便在距离内存在其他样本eps,这些样本被定义为核心样本的邻居。这告诉我们核心样本位于向量空间的稠密区域。 簇中还具有一组非核心样本,它们是簇中核心样本的邻居的样本,但本身并不是核心样本。 显然,这些样本位于簇的边缘。
根据定义,任何核心样本都是簇的一部分,任何不是核心样本并且和任意一个核心样本距离都大于eps 的样本将被视为异常值。
参数min_samples 主要控制算法对噪声的容忍度(当处理大型噪声数据集时, 需要考虑增加该参数的值), 如何选择适当的eps 对具体地数据集和距离函数非常关键,通常不能使用默认值。参数eps控制了点地领域范围。如果取值太小,大多数数据并不会被聚类(并将“噪音”标记为-1); 如果取值太大,可能会导致相近的多个簇被合并成一个,并最终将整个数据集分配到单个簇返回。文献上已经讨论过了一些启发式(heuristics)参数选择方法。例如,在最近邻距离图种,基于Knee的参数选择方式(如下面的参考文献中所讨论的)。
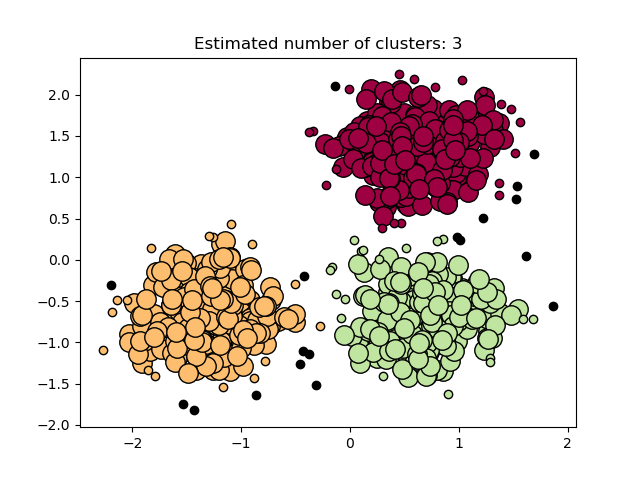
在下图中,颜色表示簇成员属性,大圆圈表示算法找到的核心样本。较小的圆圈表示仍是簇的一部分的非核心样本。 此外,下面的黑点表示异常值。
 示例:
示例:
实现
DBSCAN 算法是确定性的,当以相同的顺序给出相同的数据时总是形成相同的簇。 然而,当以不同的顺序提供数据时,结果可能不相同。首先,尽管核心样本总是被分配给相同的簇,但这些簇的标签将取决于数据中遇到这些样本的顺序。其次,更重要的是,分配给非核心样本的簇可能因数据顺序而有所不同。 当一个非核心样本到两个不同簇的核心样本的距离都小于 eps 时,就会发生这种情况。 根据三角不等式,这两个核心样本距离必须大于 eps ,否则他们将处于同一个簇中。 非核心样本将被分配给在数据传递过程中首先生成的任何簇,因此结果也将取决于数据排序。
当前版本使用 ball trees 和 kd-trees 来确定点的领域,从而避免了计算完整的距离矩阵 (就像在0.14之前的scikit-learn版本中所做的那样)。保留使用自定义指标(custom metrics)的可能性。更多细节请参照 NearestNeighbors。
在大规模样本上运行时的内存消耗
这个实现在默认情况下内存效率不高,因为在不能使用 kd-trees 或 ball-trees 的情况下情况下构建一个完整的相似度矩阵(例如,使用稀疏矩阵情况下)。这个矩阵会消耗n²个浮点数。 解决这个问题的几种机制:
使用 OPTICS 聚类算法结合 extract_dbscan方式。 OPTICS 聚类算法同样需要计算全结对矩阵(full pairwise matrix),但每次仅在内存中保持一行(内存复杂度为 n)。稀疏半径邻域图(A sparse radius neighborhood graph)(其中缺少的样本被假定为距离超出eps) 可以以高效的方式预先编译,并且可以使用 metric='precomputed'来运行 dbscan。可以对数据集进行压缩,当数据中存在准确的重复时,可以删除这些重复的数据,或者使用BIRCH。 那么对于大量的点仅需要使用相对少量的样本。然后在训练DBSCAN时,可以提供一个 sample_weight参数。
参考文献:
“A Density-Based Algorithm for Discovering Clusters in Large Spatial Databases with Noise” Ester, M., H. P. Kriegel, J. Sander, and X. Xu, In Proceedings of the 2nd International Conference on Knowledge Discovery and Data Mining, Portland, OR, AAAI Press, pp. 226–231. 1996 “DBSCAN revisited, revisited: why and how you should (still) use DBSCAN. Schubert, E., Sander, J., Ester, M., Kriegel, H. P., & Xu, X. (2017). In ACM Transactions on Database Systems (TODS), 42(3), 19.
2.3.8. OPTICS
OPTICS算法与DBSCAN算法有许多相似之处,可以认为是DBSCAN算法的推广,将eps要求从一个值放宽到一个值范围。OPTICS与DBSCAN的只要区别在于OPTICS算法建立了一个可达性图,它为每个样本分配了一个reachability_距离(可达性距离)和一个簇ordering_属性中的点;拟合模型时会分配这两个属性,用于确定簇的成员关系。如果运行OPTICS时max_eps设置为默认值inf,则可以使用cluster_optics_dbscan方法对任意给定的eps值在线性时间内针对任何给定值重复执行DBSCAN样式的簇提取。将max_eps设置为较低的值将缩短运行时间,并可以视为从每个点开始寻找其他可能的可到达点的最大邻域半径。
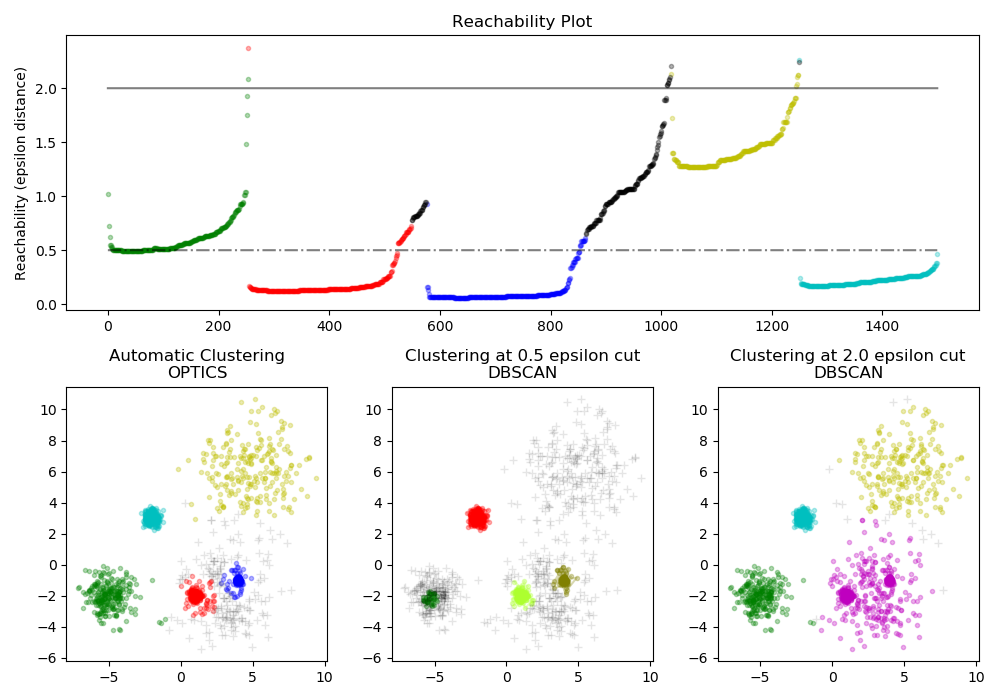
 OPTICS生成的可达性距离允许在单个数据集中进行可变密度的簇提取。如上图所示,将可达性距离和数据集
OPTICS生成的可达性距离允许在单个数据集中进行可变密度的簇提取。如上图所示,将可达性距离和数据集ordering_结合生成可达性图,其中点密度在Y轴上表示,并且对点进行排序以使附近的点相邻。在单个值处“切割”可达性图会产生类似DBSCAN的结果; “切割”上方的所有点都会被归类为噪声,每次从左到右读取时都表示新的簇。使用OPTICS进行默认的簇提取时,会查看图中的陡峭斜率以查找簇,用户可以使用参数xi定义什么算作陡峭斜率。还可以对图形本身进行其他分析,例如通过可达性图树状图生成数据的层次表示,并且可以通过cluster_hierarchy_参数访问算法检测到的聚类的层次。上面的图已经过颜色编码,因此平面空间中的簇颜色与可达性图的线性段簇匹配。请注意,蓝色和红色群集在可达性图中相邻,可以分层次地表示为较大父簇的子簇。
示例:
与DBSCAN相比
OPTICS cluster_optics_dbscan方法和DBSCAN的结果非常相似,但并不总是相同; 具体而言,是在标记离群点和噪声点方面。这部分是因为由OPTICS处理的每个密集区域的第一个样本具有大的可达性值,使得接近其区域中的其他点,因此有时将被标记为噪声而不是离群点。当它们被视为被标记为离群点或噪声的候选点时,这会影响相邻点的判断。
请注意,对于任何单个值eps,DBSCAN的运行时间往往比OPTICS短; 但是,对于不同eps 值的重复运行,单次运行OPTICS可能需要比DBSCAN更少的累积运行时间。同样重要的是要注意的是OPTICS的输出接近DBSCAN的只有eps和max_eps接近。
计算复杂度
采用空间索引树以避免计算整个距离矩阵,并允许在大量样本上有效地使用内存。可以通过metric关键字提供不同的距离度量。
对于大型数据集,可以通过HDBSCAN获得类似(但不相同)的结果 。HDBSCAN实现是多线程的,并且具有比OPTICS更好的算法运行时间复杂性,代价是更高的内存代价。对于使用HDBSCAN将耗尽系统内存的极大数据集,OPTICS将维持n(而不是n^2)内存缩放; 然而,可能需要使用max_eps参数的调优来在合理的时间内给出解。
参考文献:
“OPTICS: ordering points to identify the clustering structure.” Ankerst, Mihael, Markus M. Breunig, Hans-Peter Kriegel, and Jörg Sander. In ACM Sigmod Record, vol. 28, no. 2, pp. 49-60. ACM, 1999.
2.3.9. Birch
该Birch为给定数据构建了一个称为聚类特征树 (CFT)的树。数据本质上是被有损压缩到一组“聚类特征”节点(CF Nodes)上。CF Nodes 具有许多称为聚类特征的子簇(CF Subclusters),并且位于非终端位置的 CF 子簇可以将 CF 节点作为子节点。
CF Subclusters 保存了用于簇的必要信息,从而避免了将整个输入数据保存在内存中。这些信息包括:
子簇中的样本数。 Linear Sum - 包含所有样本和的n维向量 Squared Sum - 所有样本的L2范数的平方和。 Centroids - 为避免重复计算 linear sum / n_samples。 质心的 Squared norm。
Birch 算法有两个参数,阈值和分支因子。分支因子限制了节点中子簇的数量,而阈值则限制了新输入样本与现有子簇之间的距离。
该算法可以视为一种实例或将数据简化的方法,因为它将输入数据简化为一组直接从CFT叶子结点中获取的一组子簇。被简化的数据可以通过将其集合到全局簇 (global clusterer) 来进一步处理。可以通过n_clusters来设置global clusterer)。如果n_clusters设置为 “none”,则直接读取叶子节点中的子簇,否则全局聚类步骤会将这些子簇标记为全局簇(标签),然后将样本映射到最近的子簇的全局簇的标签。
算法描述:
一个新的样本被插入到CF树的根也就是CF节点中。然后与根的子簇合并,合并后的子簇半径最小,受阈值和分支因子的约束。如果子簇有任何子节点,则重复执行此操作直到到达叶子节点。在叶子节点中找到最近的子簇之后,将递归地更新这个子簇和父簇的属性。 如果通过合并新样本和最近的子簇得到的子簇的半径大于阈值的平方,并且子簇的数量大于分支因子,那么将临时为这个新样本分配一个空间。取两个最远的子簇,根据子簇之间的距离将子簇分为两组。 如果拆分的节点有一个父子簇(parent subcluster),并且还有空间足够容纳一个新的子簇,那么父簇会拆分成两个。如果没有空间容纳一个新的簇,那么这个节点将被再次一分为二,然后递归进行这个过程,直到到达根节点。
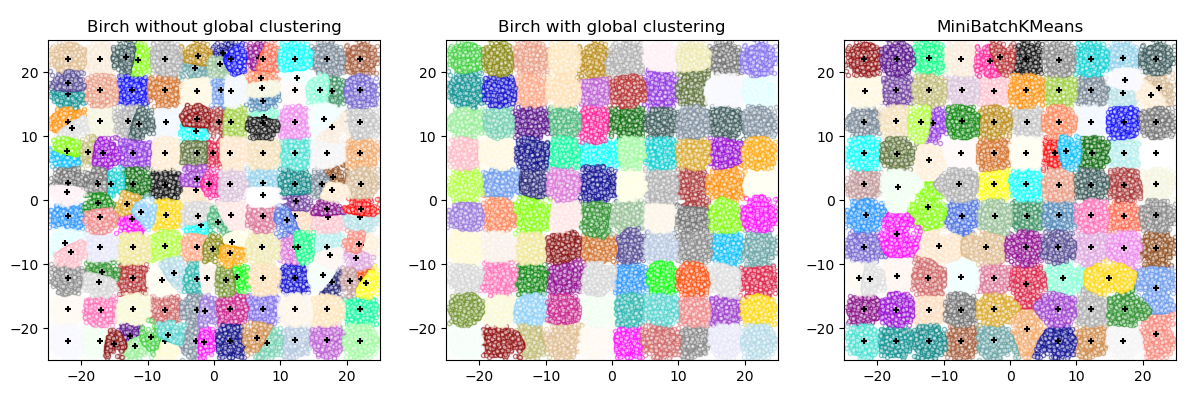
Birch or MiniBatchKMeans?
Birch 不能很好的扩展到高维数据。根据经验,如果 n_features大于20,通常使用 MiniBatchKMeans 更好。如果需要减少数据样本的数量,或者如果需要大量的子聚类作为预处理步骤或者其他, 那么Birch 比 MiniBatchKMeans 更有用。
How to use partial_fit?
为了避免对 global clustering 的计算,每次调用 partial_fit,建议进行如下操作:
初始化 n_clusters=None。通过多次调用 partial_fit训练所有数据。通过使用 brc.set_params(n_clusters=n_clusters),设置n_clusters为必需值。最后调用无参的 partial_fit, 即brc.partial_fit()执行全局聚类。
 参考资料:
参考资料:
Tian Zhang, Raghu Ramakrishnan, Maron Livny BIRCH: An efficient data clustering method for large databases. https://www.cs.sfu.ca/CourseCentral/459/han/papers/zhang96.pdf Roberto Perdisci JBirch - Java implementation of BIRCH clustering algorithm https://code.google.com/archive/p/jbirch
2.3.10. 聚类性能度量
评估聚类算法的性能并不像统计错误数量或计算监督分类算法的准确率和召回率那么简单。特别是任何度量指标不应考虑簇标签的绝对值,而是如果这个聚类方式分离的数据类似与一些真实类或满足某些假设,这样在同于一个相似性度量下,属于同一个类内的成员比不同类的成员更加类似。
2.3.10.1. 调整后的兰德指数
已知真实簇标签分配 labels_true 和我们的聚类算法是基于相同样本所得到的 labels_pred,**调整后的兰德指数是一个函数,它测量两个簇标签分配的值的 **相似度 ,忽略排列(permutations)和 机会归一化(chance normalization):
>>> from sklearn import metrics
>>> labels_true = [0, 0, 0, 1, 1, 1]
>>> labels_pred = [0, 0, 1, 1, 2, 2]
>>> metrics.adjusted_rand_score(labels_true, labels_pred)
0.24...
在预测的标签列表中重新排列 0 和 1, 把 2 重命名为 3, 得到相同的得分:
>>> labels_pred = [1, 1, 0, 0, 3, 3]
>>> metrics.adjusted_rand_score(labels_true, labels_pred)
0.24...
此外, adjusted_rand_score 是 对称的(symmetric) : 交换参数不会改变得分。它可以作为一种 共识度量(consensus measure):
>>> metrics.adjusted_rand_score(labels_pred, labels_true)
0.24...
完美标签的得分为1.0:
>>> labels_pred = labels_true[:]
>>> metrics.adjusted_rand_score(labels_true, labels_pred)
1.0
不良标签 (e.g. 独立标签(independent labelings)) 的得分是负数或接近于0.0:
>>> labels_true = [0, 1, 2, 0, 3, 4, 5, 1]
>>> labels_pred = [1, 1, 0, 0, 2, 2, 2, 2]
>>> metrics.adjusted_rand_score(labels_true, labels_pred)
-0.12...
2.3.10.1.1. 优点
对于 n_clusters和n_samples的任何值,(随机(统一)标签分配的 ARI 得分接近于 0.0)(这并不适用于原始的 Rand index 或者 V-measure 的情况)。Bounded range(有界范围) [-1, 1]: 负值是不良标签的得分, 类似的聚类结果有一个正的 ARI 值, 1.0 是完美的匹配得分。 没有对簇的结构作任何假设(No assumption is made on the cluster structure): 可以用于比较聚类算法,如: k-means 的簇是 isotropic blob shapes, 谱聚类算法的簇是 folded shapes。
2.3.10.1.2. 缺点
与惯性相反,**ARI需要了解真实簇信息,**而在实践中几乎是不可用的,或者需要人工标注者手动分配(如在监督学习环境中)。
但是,
示例:
聚类表现评估中的机会调整: 分析数据集大小对随机分配的聚类度量值的影响。
2.3.10.1.3. 数学表达
如果 C 是一个真实簇的标签分配, K 是簇的个数,定义 和 为:
,在 C 中的相同集合与 K 中的相同集合中的元素对数 ,在 C 中的不同集合与 K 中的不同集合中的元素对数
原始(未排序)的 兰德指数 由下式给出:
其中 是数据集中可能的数据对总数(未排序)。
然而,RI评分并不能保证随机标签分配会得到接近于零的值(特别是,如果簇的数量与样本数量具有相同的数量级)。
为了抵消这种影响,我们可以通过定义 adjusted Rand index 来低估(discount)随机标签的预期 RI
,如下所示:参考资料:
Comparing Partitions L. Hubert and P. Arabie, Journal of Classification 1985 Wikipedia entry for the adjusted Rand index
2.3.10.2. 基于互信息(mutual information)的得分
已知真实簇的标签分配 labels_true 和我们的聚类算法基于相同样本所得到的 labels_pred, 互信息 是度量两个标签分配的 一致性的函数,忽略排列。这种度量方案有两个不同的归一化版本,Normalized Mutual Information(NMI) 和 Adjusted Mutual Information(AMI)。NMI 经常在文献中使用,而 AMI 最近才提出的,并且 随偶然性而归一化(normalized against chance) :
>>> from sklearn import metrics
>>> labels_true = [0, 0, 0, 1, 1, 1]
>>> labels_pred = [0, 0, 1, 1, 2, 2]
>>> metrics.adjusted_mutual_info_score(labels_true, labels_pred)
0.22504...
在预测的标签列表中重新排列 0 和 1, 把 2 重命名为 3, 得到相同的得分:
>>> labels_pred = [1, 1, 0, 0, 3, 3]
>>> metrics.adjusted_mutual_info_score(labels_true, labels_pred)
0.22504...
全部的, mutual_info_score, adjusted_mutual_info_score 和 normalized_mutual_info_score 是对称的: 交换参数不会更改得分。因此,它们可以用作共识度量(consensus measure):
>>> metrics.adjusted_mutual_info_score(labels_pred, labels_true)
0.22504...
完美标签得分是 1.0:
>>> labels_pred = labels_true[:]
>>> metrics.adjusted_mutual_info_score(labels_true, labels_pred)
1.0
>>> metrics.normalized_mutual_info_score(labels_true, labels_pred)
1.0
而 mutual_info_score不是这样,因为它更难判断:
>>> metrics.mutual_info_score(labels_true, labels_pred)
0.69...
不良标签 (例如(无相关标签)independent labelings) 具有非正分数:
>>> labels_true = [0, 1, 2, 0, 3, 4, 5, 1]
>>> labels_pred = [1, 1, 0, 0, 2, 2, 2, 2]
>>> metrics.adjusted_mutual_info_score(labels_true, labels_pred)
-0.10526...
2.3.10.2.1. 优点
Random (uniform) label assignments have a AMI score close to 0.0(随机(统一)标签分配的AMI评分接近0.0) 适用于 n_clusters和n_samples取任何值(这不适用于原始 Rand index 或 V-measure 的情况)。Upper Bound of 1(上界1) 数值趋近 0 说明两个标签分配之间是独立的;而数值趋近于 1 时, 表示两者显著一致。 此外,如果AMI的取值恰好是 1 时, 说明两个标签分配是完全相等的(无论是否排列过)。
2.3.10.2.2. 缺点
与惯量相反,MI-based measures 需要先得知 ground truth classes ,而在实践中几乎从来没有使用过,或者需要人工标注者手动分配(如在监督学习环境中)。
然而,基于 MI 的测量方式(MI-based measures)也可在完全无监督的情况下作为聚类模型选择过程中共识索引的一个构建模块。
NMI 和 MI 不能进行使得随机标签度量的得分为0的调整。
示例:
聚类表现评估中的机会调整: 分析数据集大小对随机分配聚类度量值的影响。 此示例还包括 Adjusted Rand Index。
2.3.10.2.3. 数学公式
假设两个标签分配(在相同的 N 个对象中进行), 和 。 它们的熵是一个分区集合的不确定性量,被定义为:
其中: 是从 中选取的对象,选取对象落入类 的概率。同样对于:
采用 , 和 之间的mutual information (MI) 由下式计算:
其中 是随机选择的对象同时落入两个类的概率 和
也可以用设定的基数表达式表示:
normalized mutual可以定义为:
mutual information 的值以及归一化变量的值都不会随着随机标签度量进行调整,但是会随着不同的簇标签数量的增加而增加,不管标签分配之间的 “mutual information” 的实际数量是多少。
可以用以下公式[VEB2009]来计算 mutual information 的期望值。在这个方程式中 , 中元素的数量) 和 (中元素的数量).
使用期望值,然后可以使用与调整后的兰德指数相似的形式来计算调整后的mutual information:
对于归一化互信息和调整互信息,归一化值通常是每个聚类熵的某个广义均值。存在在各种广义的手段,并且不存在一种确定的规则确定某种方法优于其他方法。这个决定很大程度上根据不同领域有不同方法;例如,在社区检测算法(Community Detection)中,算术平均是最为常见。每一种归一化方法都提供了定性相似行为(qualitatively similar behaviours)[YAT2016]。在我们的实现中,这由average_method参数控制的。
Vinh等(2010)用平均法命名NMI和AMI的变体[VEB2010]。它们的“ sqrt”和“ sum”平均值是几何和算术平均值;我们使用这些更广泛的通用名称。
参考文献:
Strehl, Alexander, and Joydeep Ghosh (2002). “Cluster ensembles – a knowledge reuse framework for combining multiple partitions”. Journal of Machine Learning Research 3: 583–617. doi:10.1162/153244303321897735.
VEB2009Vinh, Epps, and Bailey, (2009). “Information theoretic measures for clusterings comparison”. Proceedings of the 26th Annual International Conference on Machine Learning - ICML ‘09. doi:10.1145/1553374.1553511. ISBN 9781605585161.
VEB2010Vinh, Epps, and Bailey, (2010). “Information Theoretic Measures for Clusterings Comparison: Variants, Properties, Normalization and Correction for Chance”. JMLR http://jmlr.csail.mit.edu/papers/volume11/vinh10a/vinh10a.pdf
YAT2016Yang, Algesheimer, and Tessone, (2016). “A comparative analysis of community detection algorithms on artificial networks”. Scientific Reports 6: 30750. doi:10.1038/srep30750.
2.3.10.3. 同质性,完整性和 V-measure
已知真实簇的标签分配,可以使用条件熵(conditional entropy)分析定义一些直观的度量(intuitive metric)。
特别是 Rosenberg 和 Hirschberg (2007) 为任何簇的分配定义了以下两个理想的目标:
同质性(homogeneity): 每个簇只包含一个类的成员 完整性(completeness): 给定类的所有成员都分配给同一个簇。
我们可以把这些概念转化为得分 homogeneity_score 和 completeness_score 。两者均在 0.0 以下 和 1.0 以上(越高越好):
>>> from sklearn import metrics
>>> labels_true = [0, 0, 0, 1, 1, 1]
>>> labels_pred = [0, 0, 1, 1, 2, 2]
>>> metrics.homogeneity_score(labels_true, labels_pred)
0.66...
>>> metrics.completeness_score(labels_true, labels_pred)
0.42...
称为 V-measure 的调和平均数由 v_measure_score计算得出:
>>> metrics.v_measure_score(labels_true, labels_pred)
0.51...
该函数的公式如下:
beta 默认为1.0,但对于beta小于1时,为:
>>> metrics.v_measure_score(labels_true, labels_pred, beta=0.6)
0.54...
更大的beta权重将提高同质性,当使用大于1的beta值时:
>>> metrics.v_measure_score(labels_true, labels_pred, beta=1.8)
0.48...
更大的beta权重将提高完整性。
V-measure 实际上等价于上面讨论的 mutual information (NMI) , 仅聚合函数(aggregation function)是算术均值[B2011]。
同质性, 完整性 和 V-measure 可以使用 homogeneity_completeness_v_measure进行计算,计算方法如下:
>>> metrics.homogeneity_completeness_v_measure(labels_true, labels_pred)
...
(0.66..., 0.42..., 0.51...)
以下聚类分配稍微好一些,因为它是同质但并不完整:
>>> labels_pred = [0, 0, 0, 1, 2, 2]
>>> metrics.homogeneity_completeness_v_measure(labels_true, labels_pred)
(1.0, 0.68..., 0.81...)
注意:
v_measure_score是对称的:可用于评估同一数据集上两个独立的标签分配。
completeness_score和homogeneity_score的情况并非如此:两者都受以下关系约束:homogeneity_score(a, b) == completeness_score(b, a)
2.3.10.3.1. 优点
Bounded scores(有界分数): 0.0 是最坏的, 1.0 是一个完美的分数. 直观解释: 具有不良 V-measure 的聚类可以用 在同质性和完整性方面进行定性分析 ,以更好地感知到标签分配所造成的“错误”类型。 No assumption is made on the cluster structure(对簇的结构没有作出任何假设): 可以用于比较不同类的聚类算法,例如: k-means 和 spectral clustering algorithms(谱聚类算法)间的比较。虽然,前者的簇是isotropic blob shapes, 后者的簇是 folded shapes。
2.3.10.3.2. 缺点
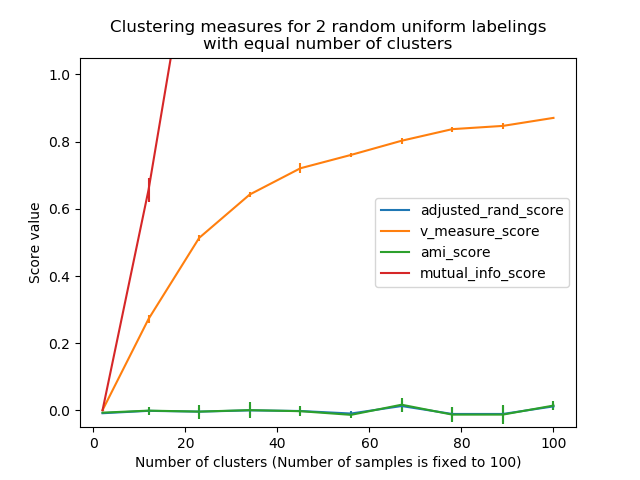
先前引入的度量标准并不针对随机标记进行标准化: 这意味着,根据样本数量,簇数量和标定过的真实数据类数量,完全随机的标注方式并不总是产生同质性,完整性 和 v-measure 的相同值。特别是特别是当簇数量很大时,随机标记不会产生零分。
当样本数量超过 1000且簇的数量小于 10 时,可以安全地忽略此问题。对于较小的样本数量或者较大数量的簇,使用 adjusted index (例如 Adjusted Rand Index (ARI))。
 这,而实践中却几乎不可用,或者需要或需要人工标注者人工分配(如在受监督的学习环境中)。
这,而实践中却几乎不可用,或者需要或需要人工标注者人工分配(如在受监督的学习环境中)。
| 示例: |
|---|
| 聚类表现评估中的机会调: 分析数据集大小对随机分配聚类度量值的影响。 |
2.3.10.3.3. 数学表达
同质性和完整性的得分由下面公式给出:
其中是给定簇分配的类的条件熵 ,由下式给出:
是 已聚合的类的熵 (entropy of the classes),并且由下式给出:
个样本总数, 和 分别属于 类 和 簇 的样本数,最后 分配给 簇 的类, 的样本数。
给定类分配的簇的条件熵(conditional entropy of clusters given class) 和 簇的熵 以对称的形式 义。
Rosenberg 和 Hirschberg 进一步定义 V-measure 作为 同质性和完整性的调和均值:
参考资料
V-Measure: A conditional entropy-based external cluster evaluation measure Andrew Rosenberg and Julia Hirschberg, 2007 [B2011] Identication and Characterization of Events in Social Media, Hila Becker, PhD Thesis.
2.3.10.4. Fowlkes-Mallows 得分
当已标定样本的真实类分配已知时,可以使用 Fowlkes-Mallows 指数 (sklearn.metrics.fowlkes_mallows_score) 。Fowlkes-Mallows 得分 FMI 被定义为 成对的准确率和召回率的几何平均值:
其中 TP 是 真正例(True Positive) 的数量(即真标签组和预测标签组中属于相同簇的点对数),FP 是 假正例(False Positive) (即不在预测标签组,仅在真标签组中属于同一簇的点对数),FN 是 假负例(False Negative) 的数量(即不在真实标签组中,仅在预测标签组中属于同一簇的点对数)。
得分范围为 0 到 1。较高的值表示两个簇之间的良好相似性。
>>> from sklearn import metrics
>>> labels_true = [0, 0, 0, 1, 1, 1]
>>> labels_pred = [0, 0, 1, 1, 2, 2]Copy
>>> metrics.fowlkes_mallows_score(labels_true, labels_pred)
0.47140...Copy
在预测的标签列表中重新排列 0 和 1, 把 2 重命名为 3, 得到相同的得分:
>>> labels_pred = [1, 1, 0, 0, 3, 3]
>>> metrics.fowlkes_mallows_score(labels_true, labels_pred)
0.47140...Copy
完美的标签得分是 1.0:
>>> labels_pred = labels_true[:]
>>> metrics.fowlkes_mallows_score(labels_true, labels_pred)
1.0Copy
不良标签(例如,无相关标签)的得分为 0:
>>> labels_true = [0, 1, 2, 0, 3, 4, 5, 1]
>>> labels_pred = [1, 1, 0, 0, 2, 2, 2, 2]
>>> metrics.fowlkes_mallows_score(labels_true, labels_pred)
0.0
2.3.10.4.1. 优点
随机(统一)标签分配的FMI评分接近0.0) 适用于 n_clusters和n_samples取任何值(但并不适用于原始的Rand index 或 V-measure )。Upper Bound of 1: 数值趋近于0 ,是说明两个标签分配在很大程度上是独立的;而数值趋近于 1 时, 表示两者之间有着极高的相似度。 甚至,当FMI的取值正好是 1 时, 表示两个标签分配是完全相等的(无论是否排列)。 没有对簇的结构作出任何假设): 可以用于比较不同类的聚类算法,例如: k-means 和 spectral clustering algorithms(谱聚类算法)间的比较。k-means的簇是isotropic blob shapes, 谱聚类算法的簇是 folded shapes。
2.3.10.4.2. 缺点
与惯量相反,基于 FMI 的测量方案需要已标注的真数据类 ,而在实践中几乎不可用,或者需要人工标注者手动分配(在监督学习学习环境中)。
参考资料
E. B. Fowkles and C. L. Mallows, 1983. “A method for comparing two hierarchical clusterings”. Journal of the American Statistical Association. http://wildfire.stat.ucla.edu/pdflibrary/fowlkes.pdf Wikipedia entry for the Fowlkes-Mallows Index
2.3.10.5. Silhouette 系数
如果真实簇标签不知道,则必须使用模型本身进行度量。Silhouette 系数 (sklearn.metrics.silhouette_score) 这种度量的一个示例,其中较高的 Silhouette 系数得分和具有更好定义的聚类的模型有关。Silhouette 系数根据每个样本进行定义,由两个得分组成:
a: 样本与同一类别中所有其他点之间的平均距离。 b: 样本与 下一个距离最近的簇中的所有其他点之间的平均距离。
给出单个样本的 Silhouette 系数 s :
其中每个样本的 Silhouette 系数的平均值可以使用一组样本的 Silhouette 系数。
>>> from sklearn import metrics
>>> from sklearn.metrics import pairwise_distances
>>> from sklearn import datasets
>>> X, y = datasets.load_iris(return_X_y=True)
在正常使用情况下,将 Silhouette 系数应用于聚类结果的分析。
>>> import numpy as np
>>> from sklearn.cluster import KMeans
>>> kmeans_model = KMeans(n_clusters=3, random_state=1).fit(X)
>>> labels = kmeans_model.labels_
>>> metrics.silhouette_score(X, labels, metric='euclidean')
0.55...
参考资料:
Peter J. Rousseeuw (1987). “Silhouettes: a Graphical Aid to the Interpretation and Validation of Cluster Analysis”. Computational and Applied Mathematics 20: 53–65. doi:10.1016/0377-0427(87)90125-7.
2.3.10.5.1. 优点
不正确的聚类得分为 -1 ,高密度聚类得分为 +1 。0 附近的分数表示重叠的聚类。 当簇密集且分离良好时,得分较高,这与簇的标准概念有关。
2.3.10.5.2. 缺点
凸簇的 Silhouette 系数通常比其他类型的簇更高,如使用DBSCAN 获得的基于密度的簇。
示例:
基于KMeans聚类分析使用silhouette选择聚类的数目 : 在此示例中,silhouette 分析用于为 n_clusters 选择最佳值.
2.3.10.6. Calinski-Harabaz 指数
当不知道真实簇标签时,可使用 Calinski-Harabaz 指数 (sklearn.metrics.calinski_harabaz_score)(也称为方差比准则)来评估模型,其中较高的 Calinski-Harabaz 得分和能够更好定义的聚类模型有关。
该指数是通过簇间色散平均值(between-clusters dispersion mean)与簇内色散之间(within-cluster dispersion)的比值给出的(其中,离散度定义为距离平方的总和):
>>> from sklearn import metrics
>>> from sklearn.metrics import pairwise_distances
>>> from sklearn import datasets
>>> X, y = datasets.load_iris(return_X_y=True)
在正常使用中,将 Calinski-Harabasz 指数应用于聚类分析的结果:
>>> import numpy as np
>>> from sklearn.cluster import KMeans
>>> kmeans_model = KMeans(n_clusters=3, random_state=1).fit(X)
>>> labels = kmeans_model.labels_
>>> metrics.calinski_harabasz_score(X, labels)
561.62...
2.3.10.6.1. 优点
当群集密集且分隔良好时,分数会更高,这与群集的标准概念有关。 分数计算迅速。
2.3.10.6.2. 缺点
凸形群集的Calinski-Harabasz索引通常比其他群集概念更高,例如通过DBSCAN获得的基于密度的群集。
2.3.10.6.3. 数学公式
对于 簇,Calinski-Harabaz 得分 是通过簇间色散平均值(between-clusters dispersion mean)与 簇内色散之间(within-cluster dispersion)的比值给出的:
其中 是组间色散矩阵(between group dispersion matrix), 是簇内色散矩阵(within-cluster dispersion matrix):
为簇 中的点集, 为簇 的中心, 为 的中心, 为簇 中的点数。
参考文献
Caliński, T., & Harabasz, J. (1974). “A Dendrite Method for Cluster Analysis”. Communications in Statistics-theory and Methods 3: 1-27. doi:10.1080/03610927408827101.
2.3.10.7. Davies-Bouldin Index
如果不知道真实簇标签,则可以使用Davies-Bouldin指数sklearn.metrics.davies_bouldin_score度量模型,其中较低的Davies-Bouldin指数与具有更好簇间分割表现的模型。
该指数表示簇之间的平均“相似度”,其中相似度是将簇之间的距离与簇本身的大小进行比较的度量。
零是最低的分数。值越接近零表示更好的分割。
在正常使用中,将Davies-Bouldin索引应用于簇分析的结果,如下所示:
>>> from sklearn import datasets
>>> iris = datasets.load_iris()
>>> X = iris.data
>>> from sklearn.cluster import KMeans
>>> from sklearn.metrics import davies_bouldin_score
>>> kmeans = KMeans(n_clusters=3, random_state=1).fit(X)
>>> labels = kmeans.labels_
>>> davies_bouldin_score(X, labels)
0.6619...
2.3.10.7.1. 优点
BDI 的计算比 Silhouette scores 要简单。 该索引只计算数据集固有的数量和特征。
2.3.10.7.2. 缺点
凸簇(convex clusters)的 DBI 通常比其他类型的簇更高,例如通过 DBSCAN 获得的基于密度的簇。 在一般情况下, 质心距离只能使用欧氏空间内的距离度量来衡量。
2.3.10.7.3. 数学公式
该指数被定义为每个簇 ()和它的最大相似度 之间的平均相似度,在该指数的上下文里,:
, 簇 内每个点和簇心的平均距离 -- 也称簇直径。
, 簇质心 和 之间的距离。
以下是一个简单构建 的方法,使得它具有非负性和对称性:
然后将Davies-Bouldin索引定义为:
参考文献
Davies, David L.; Bouldin, Donald W. (1979). “A Cluster Separation Measure” IEEE Transactions on Pattern Analysis and Machine Intelligence. PAMI-1 (2): 224-227. doi:10.1109/TPAMI.1979.4766909. Halkidi, Maria; Batistakis, Yannis; Vazirgiannis, Michalis (2001). “On Clustering Validation Techniques” Journal of Intelligent Information Systems, 17(2-3), 107-145. doi:10.1023/A:1012801612483. Wikipedia entry for Davies-Bouldin index.
2.3.10.8. Contingency Matrix
列联矩阵(Contingency Matrix)(sklearn.metrics.cluster.contingency_matrix) 记录了每个真实/预测簇对之间的交叉基数。 列联矩阵为所有的聚类度量提供了足够的统计数据,在这些度量中样本都是独立和均匀分布的,不需要考虑某些未聚类的样本。
这是一个例子:
>>> from sklearn.metrics.cluster import contingency_matrix
>>> x = ["a", "a", "a", "b", "b", "b"]
>>> y = [0, 0, 1, 1, 2, 2]
>>> contingency_matrix(x, y)
array([[2, 1, 0],
[0, 1, 2]])
输出数组的第一行指示存在三个样本的真实簇是''a''。其中两个的预测簇是 0,一个是 1, 没有一个是 2。而第二行表示有三个样本的真实簇是‘’b‘’ 。 其中,没有一个样本的预测簇是 0, 一个是 1, 两个是 2。
用于分类的混淆矩阵(confusion matrix) 是平方列矩阵,其中行和列的顺序对应于类别列表。
2.3.10.8.1. 优点
允许检查每个真实簇在预测簇中的分布,反之亦然。 计算列联矩阵通常利用了两个聚类之间的相似性统计数据(如本文档中列出的其他相似性统计信息)。
2.3.10.8.2. 缺点
列联矩阵很容易解释小数量的簇,但对于数量较大的簇则很难解释。
没有给出一个单一的指标来做聚类优化。
参考文献

 免费 AI IDE
免费 AI IDE



更多建议: