在计算机科学中,排序算法是一项基础而重要的任务。归并排序以其高效性和稳定性而闻名于世。它通过将待排序数组一分为二,分别对两个子数组进行排序,再将排好序的子数组合并,最终得到完全有序的数组。本文将深入探讨归并排序的工作原理,以及它在实际应用中的优势。
归并排序原理
- 分治策略:归并排序采用分治的思想。它将待排序数组递归地分成两个子数组,直到每个子数组只包含一个元素,然后对这些子数组进行排序。
- 合并操作:在子数组排序完成后,归并排序将这些有序的子数组合并成一个有序的数组。合并操作是归并排序的核心步骤。
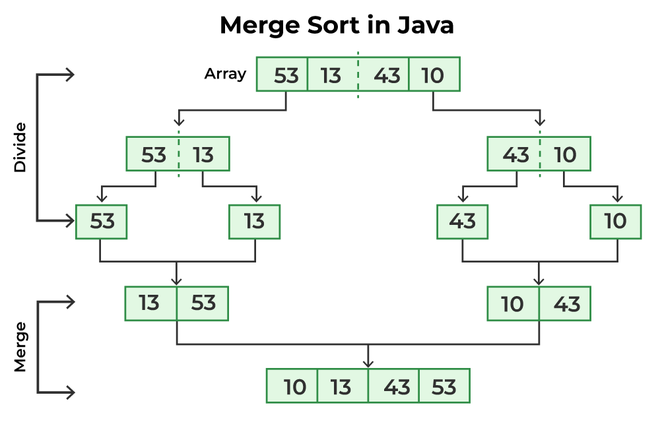
归并排序步骤
- 分割数组将待排序数组递归地分割成两个子数组,直到每个子数组只包含一个元素。
- 排序子数组对每个子数组进行排序。可以使用递归继续拆分子数组,或者使用其他排序算法如插入排序来处理较小的子数组。
- 合并子数组合并排好序的子数组,得到一个完全有序的数组。合并操作需要创建一个临时数组,用于存储合并后的结果。
- 重复合并重复步骤三,直至所有子数组都合并为一个有序的数组。
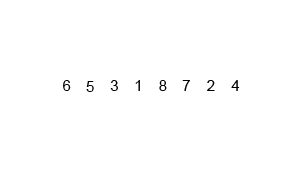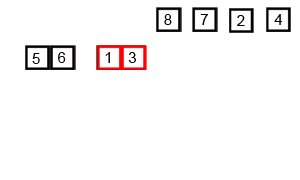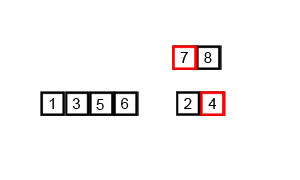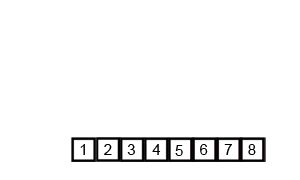
示例代码
public class MergeSort {
public static void main(String[] args) {
int[] arr = {9, 5, 1, 3, 10, 8, 2, 4, 7, 6};
mergeSort(arr, 0, arr.length - 1);
System.out.println("排序后数组: " + Arrays.toString(arr));
}
public static void mergeSort(int[] arr, int left, int right) {
if (left < right) {
int mid = (left + right) / 2;
mergeSort(arr, left, mid); // 对左半部分进行归并排序
mergeSort(arr, mid + 1, right); // 对右半部分进行归并排序
merge(arr, left, mid, right); // 合并左右两部分
}
}
public static void merge(int[] arr, int left, int mid, int right) {
int n1 = mid - left + 1;
int n2 = right - mid;
int[] L = new int[n1];
int[] R = new int[n2];
// 将数据复制到临时数组 L 和 R
for (int i = 0; i < n1; i++) {
L[i] = arr[left + i];
}
for (int j = 0; j < n2; j++) {
R[j] = arr[mid + 1 + j];
}
// 合并临时数组 L 和 R 到 arr
int i = 0, j = 0, k = left;
while (i < n1 && j < n2) {
if (L[i] <= R[j]) {
arr[k] = L[i];
i++;
} else {
arr[k] = R[j];
j++;
}
k++;
}
// 将剩余的元素复制到 arr
while (i < n1) {
arr[k] = L[i];
i++;
k++;
}
while (j < n2) {
arr[k] = R[j];
j++;
k++;
}
}
}时间复杂度和稳定性
时间复杂度:归并排序的时间复杂度为O(nlogn),其中n是待排序数组的长度。这是因为在每一层递归中,需要O(n)的时间进行合并操作,而递归的层数是O(logn)。
稳定性:归并排序是一种稳定的排序算法,即具有相同值的元素在排序后的相对顺序保持不变。
应用场景
- 大规模数据排序:归并排序适用于大规模数据的排序,因为它的时间复杂度相对稳定,不会受到数据分布的影响。
- 外部排序:归并排序适用于需要在外部存储器上进行排序的情况,因为它可以有效地利用磁盘或磁带等外部存储设备。
- 排序稳定性要求高:对于需要保持相同值元素相对顺序的排序任务,归并排序是一个理想的选择。
总结
归并排序是一种高效、稳定的排序算法,通过分治和合并的思想将排序问题划分为较小的子问题,并且能够保证排序的稳定性。它的时间复杂度为O(nlogn),适用于大规模数据的排序和需要保持排序稳定性的任务。归并排序在计算机科学领域有广泛的应用,是排序算法中的重要一员。

 免费 AI IDE
免费 AI IDE



